
题目列表(包括答案和解析)
(17)(本小题满分12分)
某班数学兴趣小组有男生和女生各3名,现从中任选2名学生去参加校数学竞赛,求:
(I)恰有一名参赛学生是男生的概率;
(II)至少有一名参赛学生是男生的概率;
(Ⅲ)至多有一名参赛学生是男生的概率。
(18)(本小题满分12分)
已知向量 =(cos
=(cos ,sin
,sin ),
),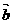 =(cos
=(cos ,-sin
,-sin ),且x∈[
),且x∈[ ,
, ].
].
(I)求 及
及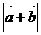 ;
;
(II)求函数f(x)= -
-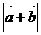 的最小值。
的最小值。
(19)(本小题满分12分)
设f(x)=ax2+bx+c(a>0),f(x)的导数为f∕(x).若|f(0)|=1,
f∕(0)=0,f(1)=0.
(I)求f(x)的解析式;
(II)对于任意的x1,x2∈[0,1],且x1≠x2.
求证:|f(x2)-f(x1)|≤2|x2-x1|与|f(x2)-f(x1)|≤1都成立。
(20)(本小题满分12分)
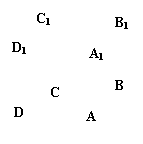 如图为一几何体的展开图:
如图为一几何体的展开图:

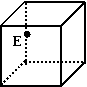
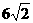 (单位:cm)
(单位:cm)
(I)沿图中虚线将它们折叠起来,是哪一种特殊几何体?并请画出其直观图,比例尺是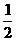 ;
;
(II)需要多少个这样的几何体才能拼成一个棱长为6cm的正方体ABCD-A1B1C1D1,请画出其示意图(需在示意图中分别表示出这种几何体);
(Ⅲ)设正方体ABCD-A1B1C1D1的棱CC1的中点为E,试求:异面直线EB与AB1所成角的余弦值及平面AB1E与平面ABC所成二面角(锐角)的余弦值。
(21)(本小题满分12分)
已知:f(x)= (x<-2),f(x)的反函数为g(x),点An(an,
(x<-2),f(x)的反函数为g(x),点An(an,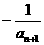 )在曲线y=g(x)上(n∈N+),且a1=1.
)在曲线y=g(x)上(n∈N+),且a1=1.
(I)求y=g(x)的表达式;
(II)证明数列{ }为等差数列;
}为等差数列;
(Ⅲ)求数列{an}的通项公式;
(Ⅳ)设bn= ,记Sn=b1+b2+……+bn,求Sn.
,记Sn=b1+b2+……+bn,求Sn.
(22)(本小题满分14分)
已知动圆与圆F1:x2+y2+6x+4=0和圆F2:x2+y2-6x-36=0都外切。
(I)求动圆圆心的轨迹C的方程;
(II)若直线L被轨迹C所截得的线段的中点坐标为(-20,-16),求直线L的方程;
(Ⅲ)若点P在直线L上,且过点P的椭圆C∕以轨迹C的焦点为焦点,试求点P在什么位置时,椭圆C∕的长轴最短,并求出这个具有最短长轴的椭圆C∕的方程。
(13)某单位有500名职工,其中不到35岁的有125人,35岁~~49岁的有280人,50岁以上的有95人。为了了解该单位职工与身体状况有关的某项指标,要从中抽取一个容量为100的样本,应该用______抽样法。
(14)从点P(-1,0)向圆(x+2)2+(y+2)2=1引切线,则切线方程为______。
(15)给出以下几个命题:
①如果空间两直线与直线L所成的角相等,那么这两直线平行。
②如果空间两直线与平面α所成的角相等,那么这两直线平行。
③到定点距离等于定长的点的轨迹是圆。
④如果一条直线和平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
⑤如果两直线a,b在平面α外,并且a⊥α,a⊥b,那么b∥α
其中,正确命题的序号为______(请将你认为正确的命题的序号全写出来)。
(16)凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,……,xn,有
 ≤f(
≤f(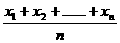 )
)
若函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB
+sinC的最大值为______。
(1)设集合A、B分别表示异面直线所成的角、直线与平面所成的角的取值 范围,则A B=
( )
B=
( )
(A)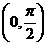 (B)
(B) (C)
(C)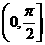 (D)
(D)
(2)函数y=x2的图象按向量 =(2,1)平移后得到的图象的函数表达式为
=(2,1)平移后得到的图象的函数表达式为
( )
(A) y=(x-2)2-1 (B) y=(x+2)2-1
(C) y=(x-2)2+1 (D) y=(x+2)2+1
(3)不等式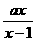 <1的解集为{x|x<1或x>2},则a=
( )
<1的解集为{x|x<1或x>2},则a=
( )
(A)2 (B)-2 (C)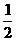 (D)-
(D)-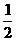
(4)设f(x)的定义域为关于坐标原点对称的区域,则f(0)=0是f(x)为奇函数的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(5)函数f(x)=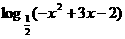 的减区间是
( )
的减区间是
( )
(A)(-∞,1) (B)(2,+∞) (C)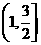 (D)
(D)
(6)给出四个函数:
(A) y=cos(2x+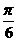 )
(B)y=sin(2x+
)
(B)y=sin(2x+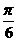 )
)
(C) y=sin( +
+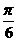 )
(D)y=tan(x+
)
(D)y=tan(x+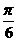 )
)
则同时具有以下两个性质的函数是 ( )
①最小正周期是π ②图象关于点(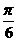 ,0)对称。
,0)对称。
(7)已知:P为抛物线y= 上的任意一点,F为抛物线的焦点,点A坐标为(1,1),则|PF|+|PA|的最小值为
( )
上的任意一点,F为抛物线的焦点,点A坐标为(1,1),则|PF|+|PA|的最小值为
( )
(A) (B)2
(C)
(B)2
(C) (D)
(D)
(8)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的最短距离为(地球半径为R) ( )
(A)R (B) (C)
(C) (D)
(D)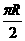
(9)设F1、F2为椭圆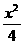 +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时, 的值为 ( )
的值为 ( )
(A)0 (B)1 (C)2 (D)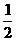
(10)我市出租车起步价为6元(起步价内行驶的里程是3Km)以后每1Km价为1.6元,则乘坐出租车的费用y(元)与行驶的里程x(Km)之间的函数图象大致为 ( )
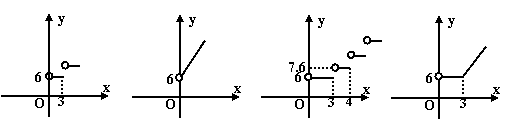
(A) (B) (C) (D)
(11)已知x,y满足约束条件 ,则z=2x+4y的最小值为( )
,则z=2x+4y的最小值为( )
(A)6 (B)-6 (C)10 (D)-10
(12)已知(1+x)+(1+x)2+(1+x)3+……+(1+x)n=a0+a1x+a2x2+a3x3+……+anxn,若a1+a2+……+an-1=29-n,则正整数n= ( )
(A)3 (B)4 (C)5 (D)6
第II卷(非选择题,共90分)
22、解:(Ⅰ)
|

又 
故 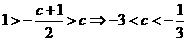 . …………………………………4分
. …………………………………4分
方程 +1=0有实根,即
+1=0有实根,即 有实根.
有实根.
故 
即 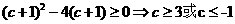 . …………………………6分
. …………………………6分
又  ,
,
得 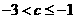 .
.
由  知
知 .
………………………………8分
.
………………………………8分
(Ⅱ)
|

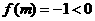 ,
,

 .
.

 .
…………………………………12分
.
…………………………………12分

 .
.

 的符号为正.
…………………………………14分
的符号为正.
…………………………………14分
21、解:(Ⅰ)法一.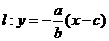 ,
,
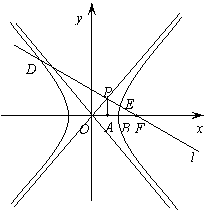
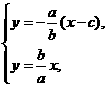 解得
解得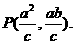 …2分
…2分

|
|
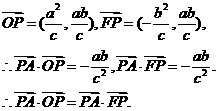
|
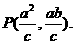
|
|

(Ⅱ)
|
|
|

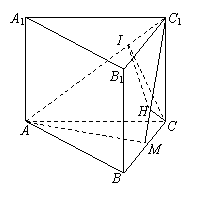
20、(甲)解: (Ⅰ) 
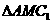 为以点M为直角顶点的等腰直角三角形,
为以点M为直角顶点的等腰直角三角形,

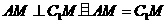 .
.
 正三棱柱
正三棱柱 ,
,

 且
且 . …………………………2分
. …………………………2分

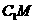 在底面内的射影为
在底面内的射影为 ,
,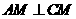 .
.

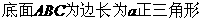 ,
,
 点
点 为
为 边的中点. ……………………………………………4分
边的中点. ……………………………………………4分
 (Ⅱ) 过点
(Ⅱ) 过点 作
作 ,
,
由(Ⅰ)知 ,
,


 ,
,

 ,
,

 , ……………………………………………6分
, ……………………………………………6分
由(Ⅰ)知, ,
, 且
且 .
.

 .
.

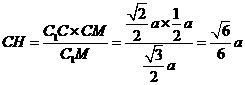 .
.
 点
点 到平面
到平面 的距离为底面边长为
的距离为底面边长为 . ………………………8分
. ………………………8分
(Ⅲ) 过点 作
作 ,
,

 ,
,

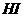 为
为 在平面
在平面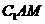 内的射影,
内的射影,

 ,
, 是二面角
是二面角 的平面角.……………10分
的平面角.……………10分
在直角三角形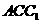 中,
中,
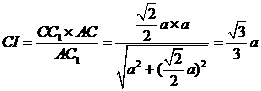 ,
,
 ,
,

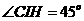 ,
,
 二面角
二面角 的大小为45O.
…………………………………12分
的大小为45O.
…………………………………12分
(乙) 解: (Ⅰ)以 为原点,建立如图所示的空间直角坐标系.……1分
为原点,建立如图所示的空间直角坐标系.……1分


 ,
……………………………3分
,
……………………………3分
 ,
,
 ,
,
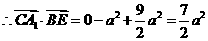 ,
,
 .
…………………5分
.
…………………5分
故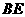 与
与 所成的角为
所成的角为 . …………………………………6分
. …………………………………6分
(Ⅱ)假设存在点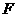 ,使
,使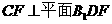 ,不妨设
,不妨设 ,
,
 ,
,
 , ……………………8分
, ……………………8分
 ……………………9分
……………………9分
由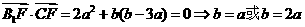 , …………………11分
, …………………11分
故当 .………………………………12分
.………………………………12分
19、解:(Ⅰ)记“摸出两个球,两球恰好颜色不同”为A,
摸出两个球共有方法 种,
………………………………2分
种,
………………………………2分
其中,两球一白一黑有 种. ………………………………4分
种. ………………………………4分
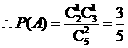 .
………………………………6分
.
………………………………6分
(Ⅱ)法一:记摸出一球,放回后再摸出一个球 “两球恰好颜色不同”为B,
摸出一球得白球的概率为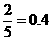 ,
,
摸出一球得黑球的概率为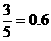 ,
……………………………8分
,
……………………………8分
“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”, ……………10分
 .
……………………………12分
.
……………………………12分
法二:有放回地摸两次,互相独立. …………………………8分
摸一次得白球的概率为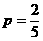 ,
……………………………10分
,
……………………………10分
 “有放回摸两次,颜色不同”的概率为
“有放回摸两次,颜色不同”的概率为

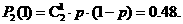 ………………………12分
………………………12分
18、解:(Ⅰ)方法一
由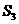 ,
,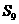 ,
,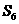 成等差数列,得
成等差数列,得 ,
………………2分
,
………………2分
若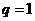 ,则
,则 ,
, ,
,
由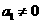 得
得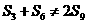 ,与题意不符,所以
,与题意不符,所以 。
……………4分
。
……………4分
由 ,得
,得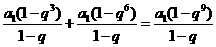 。 ………………6分
。 ………………6分
整理,得 。
。
由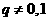 ,得
,得 。
…………………8分
。
…………………8分
(Ⅰ)方法二
由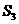 ,
,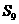 ,
,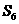 成等差数列,得
成等差数列,得 ,
…………………2分
,
…………………2分
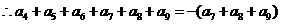 …………………4分
…………………4分
移项得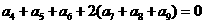
|
|

(Ⅱ) 方法一
由(1)知:
|
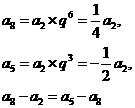
所以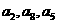 成等差数列。 …………………………………………12分
成等差数列。 …………………………………………12分
(Ⅱ) 方法二
由(1)知:
|

所以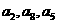 成等差数列。
…………………………………………12分
成等差数列。
…………………………………………12分
17、解: (方法一)
|
|
|
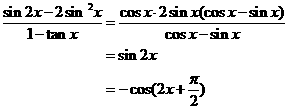
|
|

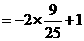
|
 .
.
(方法二)
|
|

|
|
|
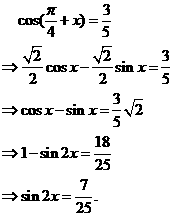
|
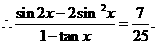
(13)33 (14)7 (15)18 (16) 只要写出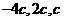 中一组即可,如
中一组即可,如 等
等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com