
题目列表(包括答案和解析)
22.(本小题满分14分)
椭圆E中心在原点O,焦点在x轴上,其离心率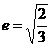 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段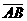 的比为2.
的比为2.
(Ⅰ)用直线l的斜率k(k≠0)表示△OAB的面积;
(Ⅱ)当△OAB的面积最大时,求椭圆E的方程.
高三数学教学质量检测试题
21.(本小题满分12分)
函数f(x)=loga(x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,Q(x-2a,-y)是函数y=g(x)图象上的点.
(Ⅰ)写出函数y=g(x)的解析式.
(Ⅱ)当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
20.(本小题满分12分)
在中国轻纺市场,当季节即将来临时,季节性服装价格呈上升趋势,设某服装开始时定价为10元,并且每周(七天)涨价2元,5周后保持20元的价格平稳销售,10周后当季节即将过去时,平均每周销价2元,直到16周末,该服装已不再销售.
(Ⅰ)试建立价格p与周次t的函数关系.
(Ⅱ)若此服装每件进价Q与周次t之间的关系Q=-0.125(t-8)2+12,t∈[0,16],
t∈ .试问该服装第几周每件销售利润L最大?
.试问该服装第几周每件销售利润L最大?
19. (本小题满分12分)
(本小题满分12分)
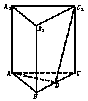
如图正三棱柱,棱都相等,D是BC上一点,AD⊥C1D.
(Ⅰ)求证:截面ADC1⊥侧面BCC1B1.
(Ⅱ)求二面角C-AC1-D的大小.
(Ⅲ)若AB=2,求A1B与截面ADC1的距离.
18.(本小题满分12分)
数列{an}中,a1=1,n≥2时,其前n项的和Sn满足Sn2=an(Sn-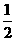 )
)
(Ⅰ)求Sn的表达式.
(Ⅱ)设bn=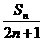 ,数列{bn}的前n项和为Tn,求
,数列{bn}的前n项和为Tn,求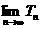 .
.
17.(本小题满分12分)
复数w满足|i-w|=1,arg(1-w)=
(Ⅰ)求w的值.
(Ⅱ)设z=cosθ+isinθ,求λ=|z-w|的最大值.
16.设α、β表示平面,l表示不在α内也不在β内的直线,存在下列三个事实①l⊥α,②l∥β,③α⊥β,若以其中两个作为条件,另一个作为结论,可构成三个命题,其中真命题是________.(要求写出所有真命题)
15.对于实数x,y,定义新运算x﹡y=ax+by+1,其中a、b是常数,等式右边是通常的加法和乘法运算,若3﹡5=15,4﹡7=28,则|﹡|=_____.
14.已知函数y=f(x)的反函数f-1(x)=logsin (x-cos2
(x-cos2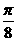 ),则方程f(x)=1的解是_______.
),则方程f(x)=1的解是_______.
13.若双曲线离心率为2,则它的两条渐近线的夹角等于_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com