
题目列表(包括答案和解析)
4. A
3.
C x y
y -x
-x y
y =0
=0
2.
D y=2sin(x+30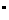 )
)
1. D
22.(本小题满分14分)
如图,设曲线C:y =x(y
=x(y 0)上的点P
0)上的点P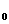 的坐标为(x
的坐标为(x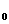 ,y
,y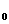 ),过P
),过P 做斜率为
做斜率为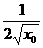 的直线,与y轴交于Q
的直线,与y轴交于Q ,过Q
,过Q 点做平行于x轴的直线与曲线C交于P
点做平行于x轴的直线与曲线C交于P (x
(x ,y
,y ),然后再过P
),然后再过P 做斜率为
做斜率为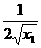 的直线交y轴于Q
的直线交y轴于Q ,过Q
,过Q 点做平行于x轴的直线与曲线C交于P
点做平行于x轴的直线与曲线C交于P (x
(x ,y
,y ),仿此,做出如下点列:
),仿此,做出如下点列:
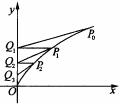 P
P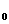 ,Q
,Q ,P
,P ,Q
,Q ,P
,P ,Q
,Q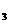 ,…,P
,…,P ,Q
,Q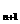 ,…。已知x
,…。已知x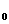 =1,设P
=1,设P (x
(x ,y
,y )。
)。
(1)
设x =f(n)(n = 0,1,2…),求f(n)的表达式;
=f(n)(n = 0,1,2…),求f(n)的表达式;
(2)
计算:S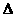 P
P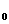 Q
Q P
P +S
+S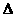 P
P Q
Q P
P +…+S
+…+S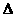 P
P Q
Q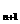 P
P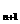 +… ;
+… ;
(3)
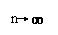 求 lim
求 lim 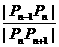 。
。
高三联考答案
21.(本小题满分12分)
某城市为了改善交通状况,需进行网络改造。已知原有道路a个标段(注:1个标段是指一个定长度的机动车道),拟增建x个标段的新路口和n个道路交叉口,n与x满足关系n = ax+b,其中b为常数。设新建1个标段道路的平均造价为k万元,新建1个道路交叉口的平均造价是新建1个标段道路的平均造价的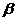 倍(
倍(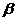
 1),n越大,路网越通畅,设路网的堵塞率为
1),n越大,路网越通畅,设路网的堵塞率为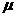 ,它与
,它与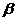 的关系为
的关系为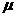 =
=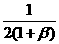 。
。
(1) 写出新建道路交叉口的总造价y(万元)与x的函数关系式;
(2) 若要求路网的堵塞率介于5%与10%之间,而且新增道路标段为原有道路标段数的25%,求新建的x个标段的总造价与新建道路交叉口的总造价之比P的取值范围;
(3) 当b =4时,在(2)的假设下,要使路网最通畅,且总造价比P最高,问原有道路标段为多少个?
20.(本小题满分12分)
已知函数f(x)=-x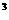 +ax在区间(0,1)上是单调递增函数。
+ax在区间(0,1)上是单调递增函数。
(1) 求实数a的取值范围;
(2) 当a取最小值时,定义数列{a }:a
}:a =b,a
=b,a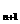 =
= f(a
f(a ),若b
),若b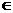 (0,1),求证a
(0,1),求证a
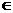 (0,1)。
(0,1)。
19.(本小题满分12分)
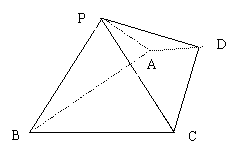 如图:已知四棱锥P-ABCD的底面为直角梯形,AD//BC,
如图:已知四棱锥P-ABCD的底面为直角梯形,AD//BC,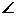 BCD=90
BCD=90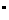 ,
,
PA=PB,PC=PD。
(1) 证明CD与平面PAD不垂直;
(2)
证明平面PAB 平面ABCD;
平面ABCD;
(3)
如果CD=AD+BC,二面角P-BC-A等于60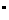 ,求二面角P-CD-A的大小。
,求二面角P-CD-A的大小。
18.(本小题满分12分)
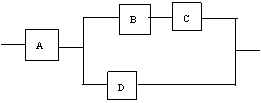
如图:用A、B、C、D四类不同的元件连接成系统N,当元件A正常工作且元件B、C都正常工作或当元件A正常工作且元件D正常工作时,系统N正常工作。已知元件A、B、C、D正常工作的概率依次为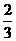 、
、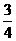 、
、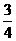 、
、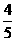 。
。
(1)
 求元件A不正常工作的概率;
求元件A不正常工作的概率;
(2) 求元件A、B、C都正常工作的概率;
(3) 求系统N正常工作的概率。
17.(本小题满分12分)
已知:定义在区间[-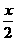 ,
,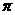 ]上的函数y = f(x)的图象关于直线x =
]上的函数y = f(x)的图象关于直线x =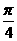 对称,当x
对称,当x
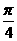 时,函数f(x)=sin x 。
时,函数f(x)=sin x 。
(1)
求f(-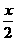 ),f(-
),f(-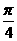 )的值;
)的值;
(2) 求y = f(x)的函数表达式;
(3)
如果关于x的方程f(x)= a有解,那么将方程在a取某一确定值时所求得的所有解的和记为M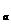 。求M
。求M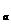 的所有可能取值及相对应的a的取值范围。
的所有可能取值及相对应的a的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com