
题目列表(包括答案和解析)
1. 已知二次函数f(x)=(x-a)(x-b)-2(a<b),并且α、β(α<β)是方程f(x)=0的两根,则a、b、α、β的大小关系是
A.α<a<b<β B.a<α<β<b
C.a<α<b<β D.α<a<β<b
 (13)用平面
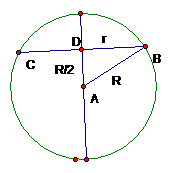
(13)用平面 截半径为R的球,如果球心到平面
截半径为R的球,如果球心到平面 的距离为
的距离为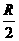 ,那么截得小圆的面积与球的表面积的比值为______________.
,那么截得小圆的面积与球的表面积的比值为______________.
讲解:设截得小圆的半径是 ,球的半径是R, 画一个轴截面图形. 在
,球的半径是R, 画一个轴截面图形. 在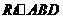 中,显然,
中,显然,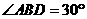 ,于是
,于是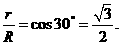
故截得小圆的面积与球的表面积的比值为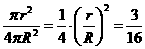 ,应填
,应填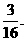
评注:题中的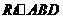 就是我们常用的三角板模型,它是高考的热门话题.
就是我们常用的三角板模型,它是高考的热门话题.
(14)函数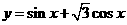 在区间
在区间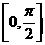 上的最小值为_____________.
上的最小值为_____________.
讲解:将函数式变形为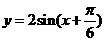 . 由
. 由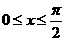 ,得
,得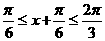 . 于是,函数的最小值为
. 于是,函数的最小值为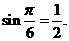 应填
应填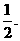
评注:如果画出函数的图象,就可看出最小值对应的点是函数图象的左端点.
(15)已知函数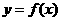 是奇函数,当
是奇函数,当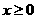 时,
时,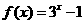 . 设
. 设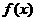 的反函数是
的反函数是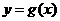 ,则
,则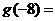 ________.
________.
讲解:易求得:当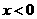 时,
时, . 这样由
. 这样由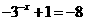 ,解得
,解得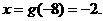 应填
应填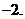
评注:反函数的定义域是原函数的值域.
(16)设P是曲线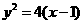 上的一个动点,则点P到点
上的一个动点,则点P到点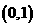 的距离与点P到
的距离与点P到 轴的距离之和的最小值是______________.
轴的距离之和的最小值是______________.
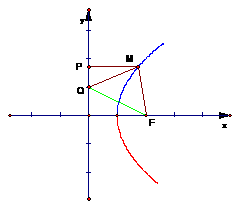 讲解:显然,
讲解:显然, 轴是抛物线
轴是抛物线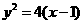 的准线,而
的准线,而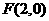 是抛物线的焦点,于是
是抛物线的焦点,于是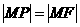 .
.
如图,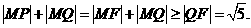
应填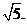
评注:如果联想到抛物线的定义,就容易找到解题的开窍点.
(1)设集合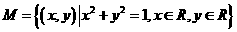 ,
,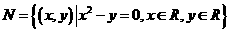 ,则集合
,则集合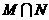 中元素的个数为( )
中元素的个数为( )
A.1 B. 2 C. 3 D. 4
讲解:在同一坐标系中,作出单位圆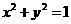 和抛物线
和抛物线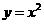 的图形,易知它们有两个交点,应选B.
的图形,易知它们有两个交点,应选B.
评注:也可通过解如下方程组求解:
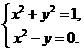
(2)函数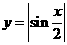 的最小正周期是( )
的最小正周期是( )
A. 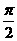 B.
B. 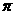 C.
C.
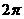 D.
D.
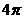
讲解:作出函数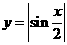 的图象,易知最小正周期是
的图象,易知最小正周期是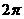 ,应选C.
,应选C.
评注:函数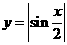 的最小正周期是函数
的最小正周期是函数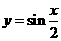 的一半.
的一半.
(3) 设数列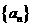 是等差数列,且
是等差数列,且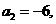
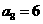 ,
,  是数列
是数列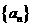 的前
的前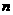 项的和,则( )
项的和,则( )
A.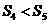 B.
B.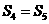 C.
C.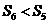 D.
D.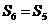
讲解:由题意得 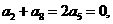 即
即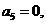 于是
于是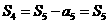 ,应选B.
,应选B.
评注:一般解法是:设等差数列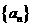 的公差是
的公差是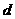 ,则有已知,得
,则有已知,得
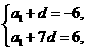 解出
解出 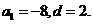 于是
于是 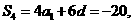
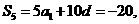
从而 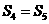 ,应选B.
,应选B.
(4) 圆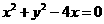 在点
在点 处的切线方程是( )
处的切线方程是( )
A. 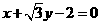 B.
B.
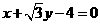
C. 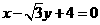 D.
D.
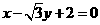
讲解:显然,点 的坐标不适合方程A, C,从而应否定A, C; 将圆的方程化为
的坐标不适合方程A, C,从而应否定A, C; 将圆的方程化为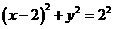 ,圆心
,圆心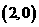 到直线
到直线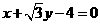 的距离为
的距离为
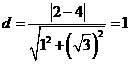 ,不是圆的半径2,故应选D.
,不是圆的半径2,故应选D.
评注:一般解法为:设圆的切线方程是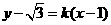 ,即
,即 ,
,
则圆心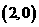 到切线
到切线 的距离为
的距离为
 解出
解出 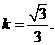
(5) 函数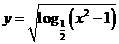 的定义域是( )
的定义域是( )
A. 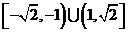 B.
B.
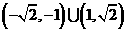
C. 
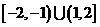 D.
D.
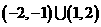
讲解: 取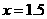 ,有
,有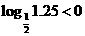 ,否定C, D; 取
,否定C, D; 取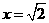 ,有
,有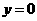 ,否定B. 应选A.
,否定B. 应选A.
评注:一般解法为:由题意得 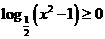 ,即
,即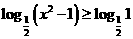 , 等价于
, 等价于 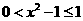 .
.
(6) 设复数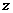 的幅角的主值为
的幅角的主值为 ,虚部为
,虚部为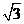 ,则
,则 ( )
( )
A. 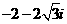 B.
B.
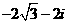
C. 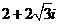 D.
D.
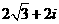
讲解:设复数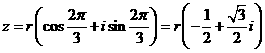 , 则有
, 则有 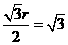 ,
,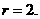 于是
于是 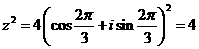
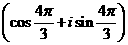 =
=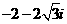 .应选A.
.应选A.
评注:也可用代数形式: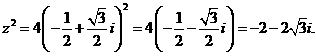
(7) 设双曲线的焦点在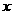 轴上,两条渐近线为
轴上,两条渐近线为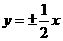 ,则双曲线的离心率
,则双曲线的离心率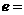 ( )
( )
A. 5 B. 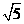 C.
C. 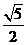 D.
D.
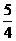
讲解:设双曲线的方程是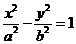 ,其两条渐近线为
,其两条渐近线为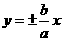 ,于是
,于是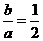 ,即有
,即有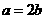 ,有
,有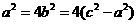 ,
,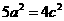 ,即
,即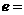
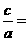
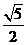 .应选C.
.应选C.
评注:双曲线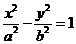 对于的两条渐近线为
对于的两条渐近线为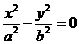 ,也就是
,也就是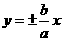 .
.
(8) 不等式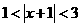 的解集为( )
的解集为( )
A. 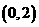 B.
B.
 C.
C. 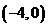 D.
D. 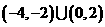
讲解:取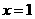 ,适合不等式,否定C; 取
,适合不等式,否定C; 取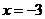 ,适合不等式,否定A, B. 应选D.
,适合不等式,否定A, B. 应选D.
评注:一种直接解法是:由原不等式得
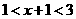 或
或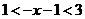 ,即
,即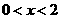 或
或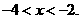
(9) 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱柱的体积为( )
A. 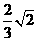 B.
B. 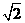 C.
C. 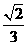 D.
D. 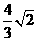
讲解:显然,侧面是等腰直角三角形,其直角边为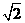 ,于是三棱柱的体积为
,于是三棱柱的体积为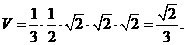 应选C.
应选C.
评注:本题的模型是正方体截下的一个,教室的一个墙角. 当中的体积计算需要转换角度思考问题.
(10) 在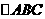 中,
中,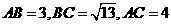 ,则边
,则边 上的高为( )
上的高为( )
A. 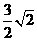 B.
B.
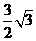 C.
C.
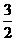 D.
D.
讲解:由余弦定理 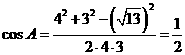 ,得
,得
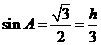 ,有
,有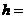
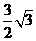 .应选B.
.应选B.
评注:请读者自己补上几何图形.
(11) 设函数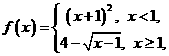 则使得
则使得 的自变量
的自变量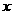 的取值范围为( )
的取值范围为( )
A.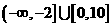 B.
B. 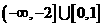
C. 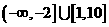 D.
D.
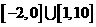
讲解:取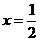 ,有
,有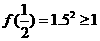 成立,否定C, D;取
成立,否定C, D;取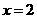 ,
,
有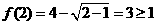 成立,否定B. 应选A.
成立,否定B. 应选A.
评注:分段函数常考常新. 本题也可给出直接解法,图象解法.
(12) 将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( )
A. 12 种 B. 24 种 C 36 种 D. 48 种
讲解: 本题可以给出一种直接解法 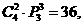 应选C.
应选C.
评注: 请读者用文字语言表述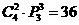 的实际意义. 再想想:解法
的实际意义. 再想想:解法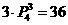 是否正确?
是否正确?
22、(14分)已知数列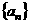 的前
的前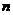 项和
项和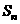 满足
满足
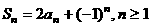
(1)
写出数列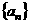 的前三项
的前三项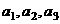 ;
;
(2)
求数列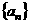 的通项公式;
的通项公式;
(3)
证明:对任意的整数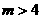 ,有
,有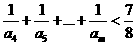 .
.
18、(12分)解方程 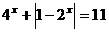
19(12分)某村计划建造一个室内面积为800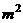 的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左、右两端与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
20(12分)三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3,
(1) 求证:AB ⊥ BC;
(2)





 设AB=BC=
设AB=BC=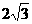 ,求AC与平面PBC所成角的大小.
,求AC与平面PBC所成角的大小.
21(12分)设椭圆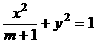 的两个焦点是
的两个焦点是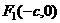 与
与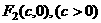 ,且椭圆上存在一点
,且椭圆上存在一点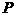 ,使得直线
,使得直线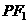 与
与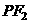 垂直.
垂直.
(1)求实数 的取值范围;
的取值范围;
(2)设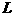 是相应于焦点
是相应于焦点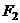 的准线,直线
的准线,直线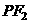 与
与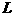 相交于点
相交于点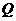 ,若
,若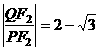 ,求直线
,求直线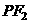 的方程.
的方程.
17、(12分)已知 为锐角,且
为锐角,且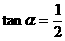 ,求
,求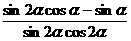 的值。
的值。
16、设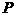 是曲线
是曲线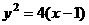 上的一个动点,则点
上的一个动点,则点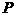 到点
到点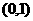 的距离与点
的距离与点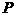 到
到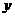 轴的距离之和的最小值为
.
轴的距离之和的最小值为
.
15、已知函数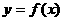 是奇函数,当
是奇函数,当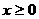 时,
时,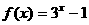 ,设
,设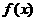 的反函数是
的反函数是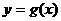 ,则
,则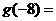 .
.
14、函数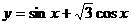 在区间
在区间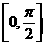 上的最小值为
.
上的最小值为
.
13、用平面 截半径为
截半径为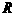 的球,如果球心到平面
的球,如果球心到平面 的距离为
的距离为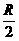 ,那么截得小圆的面积与球的表面积的比值为
.
,那么截得小圆的面积与球的表面积的比值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com