
题目列表(包括答案和解析)
4.平面内有10条直线,其中任意两条都相交,任意三条都不过同一点,它们将平面分割
成 个部分,则
个部分,则 的值为 ( )
的值为 ( )
A.54 B.55 C.56 D.92
3.把直线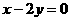 按向量
按向量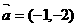 平移后,所得直线与圆
平移后,所得直线与圆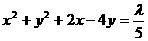 相
相
切,则实数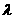 的值为 ( )
的值为 ( )
A.39 B.13 C.-21 D.-39
1.已知△ABC中,点D在BC边上,且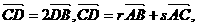 则
则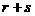 的值是( )
的值是( )
A.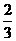 B.
B.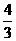 C.-3 D.0
C.-3 D.0
 2.函数
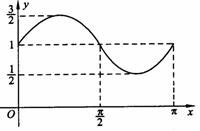
2.函数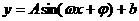 的图象如图所示,
的图象如图所示,
则它的解析式是( )
A.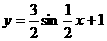 B.
B.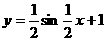
C.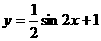 D.
D.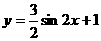
22.(本小题满分14分)
已知曲线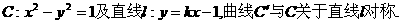
(1)求:当k=1时C′的方程;
(2)求证:对任意实数k,C与C′恒有公共点.
解:(1)设点P′(x,y)为C′上任一点,则P′关于l的对称点P(x0,y0)在C上…(1分)

(2)当l与C有公共点或C上有两不同点关于l对称时,C与C′有交点,当l与C有公共点时
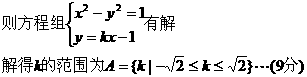
当C上存在两不同点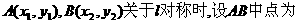
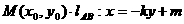 则lAB与C有交点且中点M在l上
则lAB与C有交点且中点M在l上

21.(本小题满分12分)
已知奇函数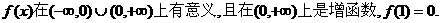
又有函数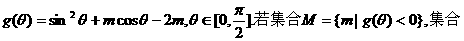
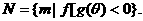 (1)求
(1)求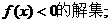 (2)求
(2)求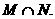
解:(1)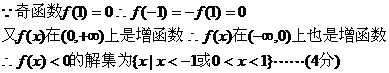
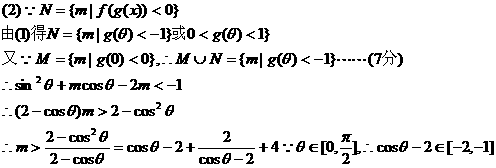

20.(本小题满分12分)
已知数列 总成等差数列.
总成等差数列.
(1)求a2,a3,a4的值;(2)求通项an;(3)计算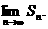
解:(1)由题意知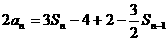

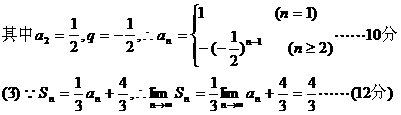
19.(本小题满分12分)如图,正四棱锥P-ABCD中,AB=2,侧棱PA与底面ABCD所成的角为60°。(1)求侧面与底面所成的二面角(锐角)的大小;
 (2)在线段PB上是否存在一点E,使得AE⊥PC,若存在,试确定点E的位置,并加以证明,若不存在,请说明理由.
(2)在线段PB上是否存在一点E,使得AE⊥PC,若存在,试确定点E的位置,并加以证明,若不存在,请说明理由.
解:(1)如图O为底面ABCD的中心
则∠PAO为PA与底面所成的角
∴∠PAO=60°
∵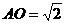 ∴
∴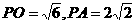 ……(2分)
……(2分)
过O作OM⊥BC于M,连PM由三垂线定理得BC⊥PM
∴∠PMO为侧面与底面所成二面角平面角……(4分)
∵OM=1,PO=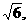
 ……6分
……6分
(2)如图建立空间直角坐标系

18.(本小题满分10分)
甲、乙两名篮球运动员,各自的投篮命中率分别为0.7与0.8,如果每人投篮两次.
(1)求甲比乙多投进一次的概率;
(2)若投进一个球得2分,未投进得0分,求两人得分之和的期望值.
解:(1)设甲进一球,乙一球没进为事件A
甲进两球,乙进一球设为事件B
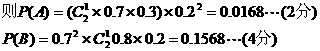
所以甲比乙多进一球的概率
P=P(A+B)=P(A)+P(B)=0.1736……(6分)
(2)设ξ表示两人投球后的得分和
|
ξ |
0 |
2 |
4 |
6 |
8 |
|
P |
0.0036 |
0.0456 |
0.2116 |
0.4256 |
0.3136 |
……(10分)
 ……(12分)
……(12分)
17.(本小题满分12分)
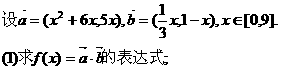
(2)求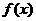 的单调增区间;(3)求
的单调增区间;(3)求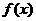 的最大值和最小值.
的最大值和最小值.
解:(1)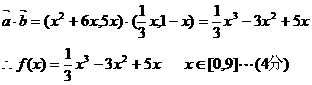
(2)
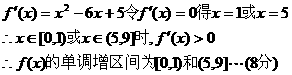

16.如图,一条直角走廊宽为1.5m,一转动灵活的平板手推车,其平板面为矩形,宽
为1m.问:要想顺利通过直角走廊,平板手推车的长度不能超过: 米.
米.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com