
题目列表(包括答案和解析)
2、下列向量组中能作为表示它们所在平面内的所有向量的基底的是 ( )
A.e1=(0,0),e2=(1,-2) B.e1=(-1,2),e2=(5,7)
C.e1=(3,5),e2=(6,10) D.e1=(2,-3),e2=(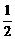 ,-
,-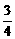 )
)
1、已知 =(4,3),向量
=(4,3),向量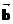 是垂直于
是垂直于 的单位向量,则
的单位向量,则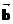 =
( )
=
( )
(A)(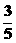 ,-
,-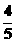 )或(-
)或(-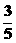 ,
,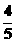 ) (B)(
) (B)(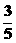 ,-
,-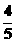 )或(-
)或(-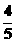 ,
,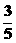 )
)
(C)(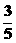 ,
,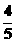 )或(-
)或(-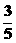 ,-
,-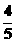 ) (D)(
) (D)(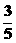 ,
,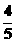 )或(
)或(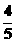 ,
,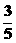 )
)
22、解:
这一命题是:已知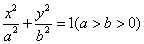 ,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为
,AA′是椭圆的长轴,P(x1,y1)是椭圆上异于A、A′的任意一点,过P点作斜率为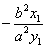 的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)|AM||A′M′|为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下:
的直线l,若直线l上的两点M、M′在x轴上的射影分别为A、A′,则(1)|AM||A′M′|为定值b2;(2)由A、A′、M′、M四点构成的四边形面积的最小值为2ab.这一命题是真命题,证明如下:
(1)不妨设A(-a,0)、 A′(a,0),由点斜式得直线l的方程是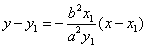 ,
,
即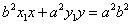 ,由射影的概念知M与A、M′与A′有相同的横坐标,
,由射影的概念知M与A、M′与A′有相同的横坐标,
由此可得, 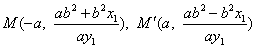 ,
,
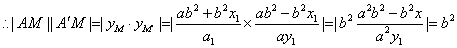 ;
;
(2)由图形分析知,不论四点的位置如何,四边形的面积S=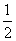 |AA′|(|AM|+|A′M′|),
|AA′|(|AM|+|A′M′|),
∵|AA′|=2a,且|AM|、|A′M′|都为正数,
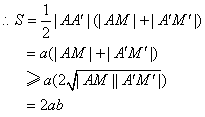
即四边形的面积的最小值为2ab.
21、解:
(1)设等差数列的首项为a1,公差为d,
等比数列的首项为b1,公比为q,
依题意有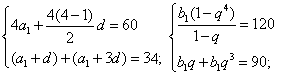
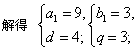 ∴ an=4n+5,bn=3n;
∴ an=4n+5,bn=3n;
(2)由(1)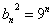 令4p+5=9n,得
令4p+5=9n,得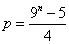 ,
,
而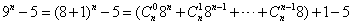 ,
,
由于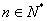 ,∴ 9n-5≥4,且上式小括号中的数为8的倍数,
,∴ 9n-5≥4,且上式小括号中的数为8的倍数,
故对于一切正整数n,使得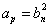 的正整数p总存在.
的正整数p总存在.
20、解:
(1)将已知图形以AD、DC、DM为相邻的三条棱补成如图所示的正方体,易知BF∥MP,
连结BQ,则∠QFB即为异面直线PM与FQ所成的角,
由正方体的性质知△BFQ是直角三角形,由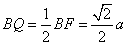 ,
,
知∠QFB=30°,即所求的角为30°;
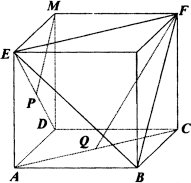
(2)由于DP=PE,所以四面体P-EBF的体积等于四面体D-EBF的一半,
所以所求的体积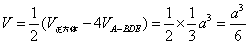 .
.
(3)由(1)异面直线PM与FQ的距离即为MP到平面BFQ的距离,
也即M点到平面BFD的距离,设这一距离为d,
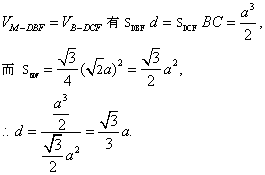
19、解:
(1)∵a∈{a|20<12a-a2},∴a2-12a+20<0,
即2<a<10,∴函数y=?logax是增函数;
(2)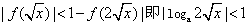 ,必有x>0,当0<x<1,
,必有x>0,当0<x<1,
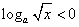 ,不等式化为
,不等式化为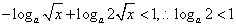 ,
,
这显然成立,此时0<x<1;
当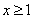 时,
时,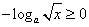 ,不等式化为
,不等式化为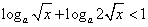 ,
,
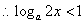 ,故
,故 ,此时
,此时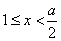 ;
;
综上所述知,使命题p为真命题的x的取值范围是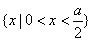 .
.
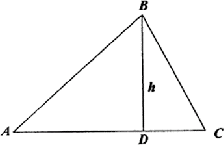
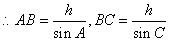 ,依题意得AB-BC=h,
,依题意得AB-BC=h,
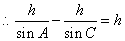 ,故得sinC-sinA=sinCsinA,
,故得sinC-sinA=sinCsinA,
又sinC和-sinA是方程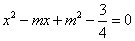 的两个根,
的两个根,
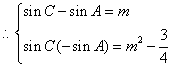 ;
;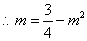 ,即
,即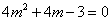 ,
,
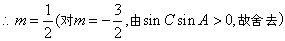 ,此时方程为
,此时方程为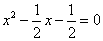 ,
,
它的两个根是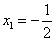 和x2=1,,∴ sinC=1,
和x2=1,,∴ sinC=1,
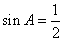 ,即有A=30°,C=90°.
,即有A=30°,C=90°.
18、解:依题意,f(0)=1,∴b=1,又∵f′(x)=x2-a,由已知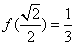 ,
,
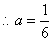 ,
,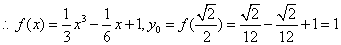 ,
,
∴所求的切线方程是 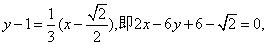
令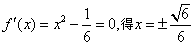 ,
,
∵当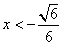 时,f′(x)>0,当
时,f′(x)>0,当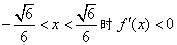 ,
,
当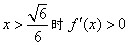 ,∴
函数f(x)有极大值
,∴
函数f(x)有极大值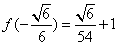 ,
,
极小值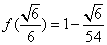 .
.
16、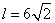 提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),
提示:由4a+2=2a-2,得a=-2, ∴平移后抛物线的焦点为F(-4,-6),
又(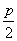 ,0)在y=x-2上,∴p=4, 由此可以求得平移公式为
,0)在y=x-2上,∴p=4, 由此可以求得平移公式为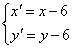 ,
,
代入原方程得平移后的抛物线方程是(y+6)2=8(x+6), 其顶点坐标为(-6,-6)) .
15、 提示:
提示: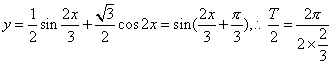 .
.
14、2 提示: 设中截面面积是S,则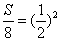 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com