
题目列表(包括答案和解析)
39. (1)
直线 方程为
方程为 ,设点
,设点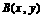 ,由
,由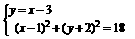 及
及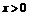 ,
,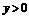 得
得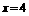 ,
,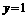 ,点
,点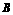 的坐标为
的坐标为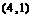 。
。
(2)由 得
得 ,设
,设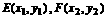 ,则
,则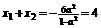 ,得
,得 。
。
(3)(解法一)设线段 上任意一点
上任意一点 坐标为
坐标为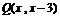 ,
,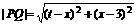 ,
,
记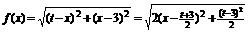
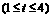 ,
,
当 时,即
时,即 时,
时,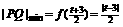 ,
,
当 ,即
,即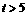 时,
时, 在
在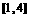 上单调递减,∴
上单调递减,∴ ;
;
 当
当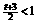 ,即
,即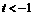 时,
时, 在
在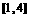 上单调递增,
上单调递增,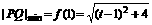 。
。
综上所述,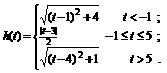
(解法二) 过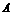 、
、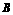 两点分别作线段
两点分别作线段 的垂线,交
的垂线,交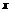 轴于
轴于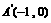 、
、 ,
,
当点 在线段
在线段 上,即
上,即 时,由点到直线的距离公式得:
时,由点到直线的距离公式得: ;
;
当点 的点在点
的点在点 的左边,
的左边,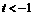 时,
时, ;
;
当点 的点在点
的点在点 的右边,
的右边,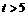 时,
时,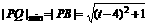 。
。
综上所述,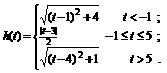
39. (04. 上海春季高考)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知倾斜角为 的直线
的直线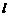 过点
过点 和点
和点 ,
, 在第一象限,
在第一象限, .
.
(1) 求点 的坐标;
的坐标;
(2) 若直线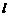 与双曲线
与双曲线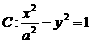
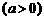 相交于
相交于 、
、 两点,且线段
两点,且线段 的中点坐标为
的中点坐标为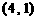 ,求
,求 的值;
的值;
(3) 对于平面上任一点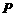 ,当点
,当点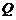 在线段
在线段 上运动时,称
上运动时,称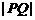 的最小值为
的最小值为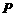 与线段
与线段 的距离. 已知点
的距离. 已知点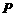 在
在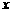 轴上运动,写出点
轴上运动,写出点 到线段
到线段 的距离
的距离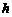 关于
关于 的函数关系式.
的函数关系式.
38.本小题主要考查直线、双曲线的方程和性质,曲线与方程的关系,及其综合应用能力,满分12分.
解:(Ⅰ)将直线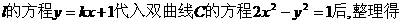
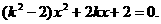 ……①
……①
依题意,直线l与双曲线C的右支交于不同两点,故

(Ⅱ)设A、B两点的坐标分别为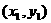 、
、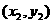 ,则由①式得
,则由①式得
 ……②
……②
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0).
则由FA⊥FB得:
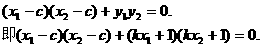
整理得
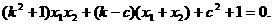 ……③
……③
把②式及 代入③式化简得
代入③式化简得
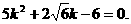
解得
可知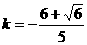 使得以线段AB为直径的圆经过双曲线C的右焦点
使得以线段AB为直径的圆经过双曲线C的右焦点
38.(2004.湖北理)(本小题满分12分)
直线 的右支交于不同的两点A、B.
的右支交于不同的两点A、B.
(I)求实数k的取值范围;
(II)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
37. 本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.满分12分.
解:(Ⅰ)设P(x1,y1),Q(x2,y2),M(x0,y0),依题意x1≠0,y1>0,y2>0.
由y= x2,
①
x2,
①
得y'=x.
∴过点P的切线的斜率k切= x1,
∴直线l的斜率kl=-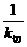 =-
=-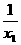 ,
,
∴直线l的方程为y- x12=-
x12=-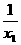 (x-x1),
(x-x1),
方法一:
联立①②消去y,得x2+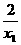 x-x12-2=0.
x-x12-2=0.
∵M是PQ的中点
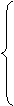 x0=
x0=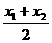 =-
=-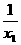 ,
,
∴
y0= x12-
x12-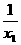 (x0-x1).
(x0-x1).
消去x1,得y0=x02+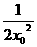 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+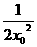 +1(x≠0).
+1(x≠0).
方法二:
由y1= x12,y2=
x12,y2= x22,x0=
x22,x0=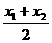 ,
,
得y1-y2= x12-
x12- x22=
x22= (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0= =kl=-
=kl=-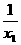 ,
,
∴x1=- ,
,
将上式代入②并整理,得
y0=x02+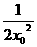 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+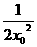 +1(x≠0).
+1(x≠0).
(Ⅱ)设直线l:y=kx+b,依题意k≠0,b≠0,则T(0,b).
分别过P、Q作PP'⊥x轴,QQ'⊥y轴,垂足分别为P'、Q',则
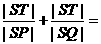
 .
.
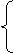 y=
y= x2
x2
由 消去x,得y2-2(k2+b)y+b2=0. ③
y=kx+b
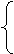 y1+y2=2(k2+b),
y1+y2=2(k2+b),
则
y1y2=b2.
方法一:
∴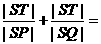 |b|(
|b|( )≥2|b|
)≥2|b|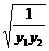 =2|b|
=2|b|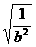 =2.
=2.
∵y1、y2可取一切不相等的正数,
∴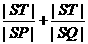 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法二:
∴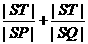 =|b|
=|b| =|b|
=|b| .
.
当b>0时,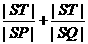 =b
=b =
= =
=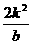 +2>2;
+2>2;
当b<0时,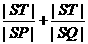 =-b
=-b =
= .
.
又由方程③有两个相异实根,得△=4(k2+b)2-4b2=4k2(k2+2b)>0,
于是k2+2b>0,即k2>-2b.
所以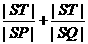 >
>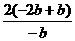 =2.
=2.
∵当b>0时,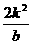 可取一切正数,
可取一切正数,
∴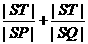 的取值范围是(2,+
的取值范围是(2,+ ).
).
方法三:
由P、Q、T三点共线得kTQ=KTP,
即 =
=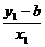 .
.
则x1y2-bx1=x2y1-bx2,即b(x2-x1)=(x2y1-x1y2).
于是b=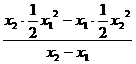 =-
=- x1x2.
x1x2.
|
|
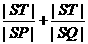 =
= =
= +
+ =
=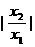 +
+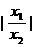 ≥2.
≥2.
∵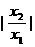 可取一切不等于1的正数,
可取一切不等于1的正数,
∴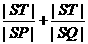 的取值范围是(2,+
的取值范围是(2,+ ).
).
36.(2004. 福建理)(本小题满分12分)
如图,P是抛物线C:y= x2上一点,直线l过点P且与抛物线C交于另一点Q.
x2上一点,直线l过点P且与抛物线C交于另一点Q.
(Ⅰ)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
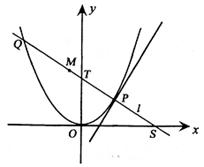 (Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求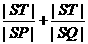 的取值范围.
的取值范围.
35、解:(1)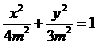
(2)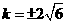 或0
或0
34.(2004.江苏)已知椭圆的中心在原点,离心率为,一个焦点是F(-m,0)(m是大于0的常数). (Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线 与y轴交于点M. 若
与y轴交于点M. 若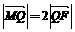 ,求直线
,求直线 的斜率.
的斜率.
33、解: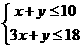 ,设
,设
当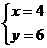 时,
时, 取最大值7万元
取最大值7万元
33.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com