3、C　 提示： .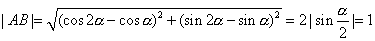

2、B　 提示：即.

22、(本小题满分14分)已知椭圆E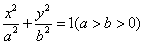：，以F1( -c，0)为圆心，以a-c 为半径作圆 　 F1，过点B2(0，b )作圆F1的两条切线，设切点为M、N.

(1)若过两个切点M、N的直线恰好经过点B1(0，-b )时，求此椭圆的离心率；

(2)若直线MN的斜率为-1 ，且原点到直线MN的距离为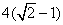，求此时的椭圆方程；　

(3)是否存在椭圆E，使得直线MN的斜率k 在区间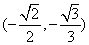内取值？若存在，求出椭圆E的离心率e 　 的取值范围；若不存在，请说明理由.

答案：一、1、C　 提示：解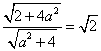得.

21、(本小题满分12分)已知函数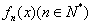具有下列性质： 　

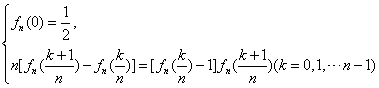
(1)当 n一定，记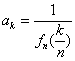，求 ak的表达式(k＝0，1，…，n )；

(2)对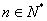，证明.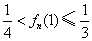

20、(本小题满分12分)某市出租车的起步价为6元，行驶路程不超过3km时，租车费为6元，若行驶路程超过 　 3km，则按每超出1km(不足1km也按1km计程)收费3元计费.设出租车一天行驶的路程数ξ(按整km数计 　 算，不足1km的自动计为1km)是一个随机变量，则其收费数η 也是一个随机变量.已知一个司机在某个 　 月中每次出车都超过了3km，且一天的总路程数可能的取值是200、220、240、260、280、300(km)，它 　 们出现的概率依次是0.12、0.18、0.20、0.20、100a2+3a、4a .

(1)求作这一个月中一天行驶路程ξ的分布列，并求ξ的数学期望和方差；

(2)求这一个月中一天所收租车费η的数学期望和方差.　

19、(本小题满分12分)如图所示，已知四边形ABCD、EADM和MDCF都是边长为a的正方形，点P、Q分别是ED和 　 AC的中点，求：

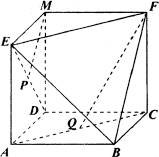
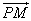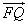(1)与所成的角；

(2)P点到平面EFB的距离；

(3)异面直线PM与FQ的距离.

18、(本小题满分12分)已知函数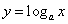，其中.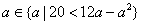

(1)判断函数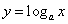的增减性；

(2)若命题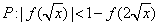为真命题，求实数x 的取值范围.

17、(本小题满分12分)设O为坐标原点，已知向量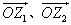分别对应复数 z1、z2，且 　(其中a∈R)，若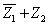可以与任意实数比较大 　 小，求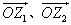的值.

16、已知抛物线y2＝2px(p>0) 的焦点在直线 y＝x-2上，现将抛物线沿向量a进行平移，且使得抛物线的焦点沿 　直线y＝x-2 移到点(2a，4a+2 )处，则平移后所得抛物线被y轴截得的弦长＝ _________.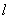

15、在ΔABC中，BC＝1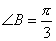，，当ΔABC的面积等于时，tanC＝________．