
题目列表(包括答案和解析)
3、使得点A(cos2α,sin2α)到点B(cosα,sinα)的距离为1的α 的一个值是( )
A.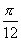 B.
B.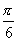
C.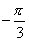 D.
D.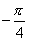
2、在等比数列{an}中,an>0 ,且a2=1-a1 ,a4=9-a3 ,则a4+a5 =( )
A.16 B.27
C.36 D.81
1、已知向量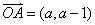 的模为
的模为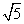 ,则实数a的值是( )
,则实数a的值是( )
A.-1 B.2
C.-1 或2 D.1或-2
22、解:
(1)圆F1的方程是(x+c)2+y2=(a-c)2,
因为B2M、B2N与该圆切于M、N点,所以B2、M、F1、N四点共圆,
且B2F1为直径,则过此四点的圆的方程是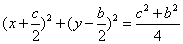 ,
,
从而两个圆的公共弦MN的方程为
cx+by+c2=(a-c)2,又点B1在MN上,∴a2+b2-2ac=0;∵b2=a2-c2,
∴2a2-2ac-c2=0,即e2+2e-2=0,∴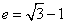 (负值舍去);
(负值舍去);
(2)由(1),MN的方程为cx+by+c2=(a-c)2,由已知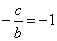 ,∴b=c,
,∴b=c,
而原点到MN的距离
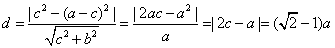 ,
,
∴a=4,b2=c2=8,所求椭圆方程是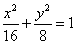 ;
;
(3)假设这样的椭圆存在,由(2)则有
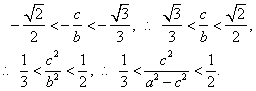 .
.
故得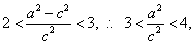 求得
求得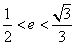 ,
,
即当离心率取值范围是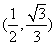 时,
时,
直线MN的斜率可以在区间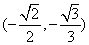 内取值.
内取值.
21、解:
(1)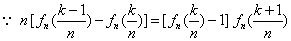 ,
,
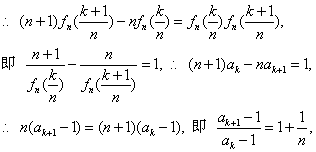
由n为定值,则数列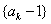 是以
是以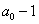 为首项,
为首项,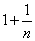 为公比的等比数列,
为公比的等比数列,
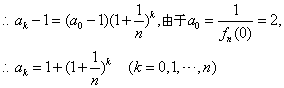
(2)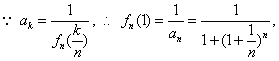

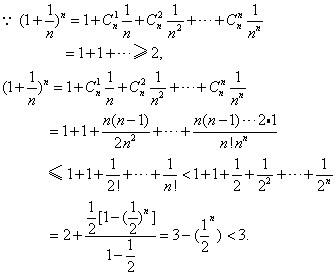
20、解:
(1)由概率分布的性质2有,0.12+0.18+0.20+0.20+100a2+3a+4a=1,
∴100a2+7a=0.3,∴ 1000a2+70a-3=0,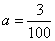 ,
,
或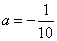 (舍去),即a=0.03,
(舍去),即a=0.03,
∴100a2+3a=0.18,4a=0.12,∴ξ的分布列为
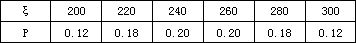
∴Eξ=200×0.12+220×0.18+240×0.20+260×0.20+280×0.18+300×0.12=250(km)
Dξ=502×0.12+302×0.18+102×0.20+102×0.20+302×0.18+502×0.12=964;
(2)由已知η=3ξ-3(ξ>3,ξ∈Z),∴ Eη=E(3ξ-3)=3Eξ-3=3×250-3=747(元),
Dη=D(3ξ-3)=32Dξ=8676.
19、解:
建立空间直角坐标系,使得D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),M(0,0,a),E(a,0,a),F(0,a,a),则由中点坐标公式得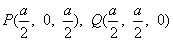 ,
,
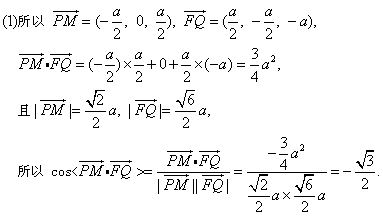
故得两向量所成的角为150°;
(2)设n=(x,y,z)是平面EFB的单位法向量,即|n|=1,n⊥平面EFB,
所以n⊥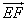 ,且n⊥
,且n⊥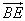 ,又
,又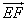 =(-a,a,0),
=(-a,a,0),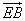 =(0,a, -a).
=(0,a, -a).
即有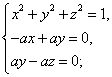 得其中的一个解是
得其中的一个解是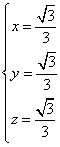 ,
,
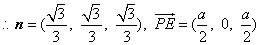 .
.
设所求距离为d,则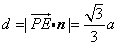 .
.
(3)设e=(x1,y1,z1)是两异面直线的公垂线上的单位方向向量,
则由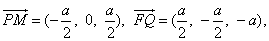 得
得
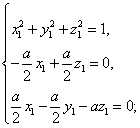 求得其中的一个
求得其中的一个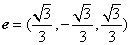 ,
,
而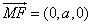 ,设所求距离为m,则
,设所求距离为m,则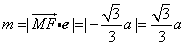
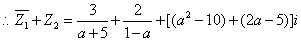 的虚部为0,
的虚部为0,
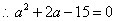 ,解得a=-5,或a=3,又分母不为零,∴a=3,
,解得a=-5,或a=3,又分母不为零,∴a=3,
此时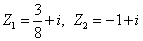 ,即
,即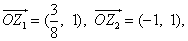
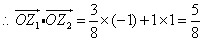 .
.
18、解:
(1)∵a∈{a|20<12a-a2},∴a2-12a+20<0,即2<a<10,∴函数y=logax是增函数;
(2) ,
,
必有x>0,当0<x<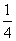 时,
时,
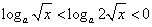 ,
,
不等式化为 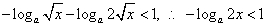 ,
,
故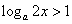 ,
,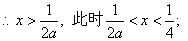
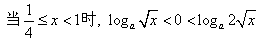 ,
,
不等式化为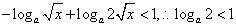 ,
,
这显然成立,此时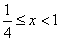 ;
;
当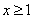 时,
时,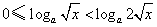 ,不等式化为
,不等式化为
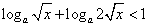 ,
,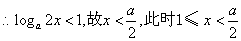 ;
;
综上所述知,使命题p为真命题的x的取值范围是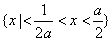 .
.
16、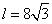 提示:由4a+2=2a-2,得a=-2,∴平移后抛物线的焦点为F(-4,-6),
提示:由4a+2=2a-2,得a=-2,∴平移后抛物线的焦点为F(-4,-6),
又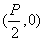 在y=x-2上,∴p=4,由此可求得平移公式为
在y=x-2上,∴p=4,由此可求得平移公式为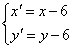 ,
,
代入原方程得平移后的抛物线方程是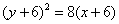 ,
,
令x=0,得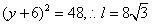
15、 提示:由面积公式
提示:由面积公式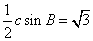 得c=4,由余弦定理得
得c=4,由余弦定理得
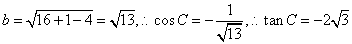 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com