(17)(本小题满分12分)

已知向量，.

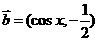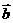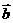(Ⅰ)当⊥时，求|+|的值；

(Ⅱ)求函数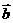＝·(－)的值域.

(18)(本小题满分12分)

如图，在直三棱柱ABC－A₁B₁C₁中，AA₁＝2，AB＝AC＝1，∠BAC＝90⁰，已知点M是BC的中点，点N在侧棱CC₁上.

(Ⅰ)当线段CN的长度为多少时，MN⊥AB₁；

(Ⅱ)若MN⊥AB₁，求B₁N与平面AB₁M所成角的余弦值.

(19)(本小题满分12分)

箱内有大小相同的6个白球，4个黑球，从中任意取出1个，记录它的颜色后再放回箱内，搅拌后再任意取出1个，记录它的颜色后又放回箱内搅拌，假设这样的抽取共进行了3次，试回答下列问题：

(Ⅰ)求事件A：“第一次取出黑球，第二次取出白球，第三次取出黑球”的概率；

(Ⅱ)若取出1只白球得2分，取出1只黑球得1分，求三次取球的总得分的数学期望.

(20)(本小题满分12分)

设数列的前n项和为，数列的前n项和为，已知，.

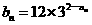(Ⅰ)求数列的通项公式；

(Ⅱ)是否存在一个最小正整数M，当时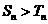，恒成立？若存在，求出这个M的值；若不存在，请说明理由.

(21)(本小题满分12分)

已知点A(0，1)，x、y∈R，m≥2，设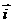，为直角坐标平面内x，y轴正方向上的单位向量，若向量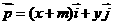，，且.

(Ⅰ)求动点M(x，y)的轨迹方程，并指出方程所表示的曲线；

(Ⅱ)设直线l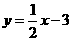：与点M的轨迹交于B、C两点，问是否存在实数m使得？若存在，求出m的值；若不存在，试说明理由.

(22)(本小题满分14分)

已知函数，当点M(x，y)在的图象上运动时，点N()在函数的图象上运动.

(Ⅰ)求的解析式；

(Ⅱ)若函数的极小值为4，求函数的单调区间；

(Ⅲ)若在时，恒成立，求参数a的取值范围.

2004年深圳市高三年级第一次调研考试

(13)已知向量，，若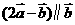，则m的值是　　 .

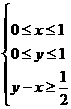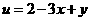(14)在条件下，则的最大值是　　　　 .

(15)设有两个命题：①关于x的不等式的解集是R，②函数是减函数.如果这两个命题中有且只有一个真命题，则实数m的取值范围是　　　　　　　 .

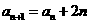(16)已知数列满足＝24，且，那么＝　　　　 .

(1)函数的反函数是

(A) 　　　(B) 　　　(C) 　　　(D)

(2)在正四面体ABCD中，BC所在直线与AD所在直线所成角是

(A) 30⁰　　　 (B)45⁰　　　 (C)60⁰　　　 (D)90⁰

(3)设曲线在点M处切线斜率为3，则点M的坐标为

(A)(0，－2)　　　 (B)(1，0)　　　 (C)(0，0)　　　 (D)(1，1)

(4)函数是

(A) 周期为的奇函数　　　　 (B) 周期为的偶函数　　　

(C) 周期为2的奇函数　　　 (D) 周期为2的偶函数

(5)棱长为1的正方体的八个顶点都在同一个球的表面上，则这个球的表面积为

(A)2　　　 (B) 3　　 (C)　　　 (D) 12

(6)在区间上递增的函数是

(A)　　 (B) 　　(C) 　　(D)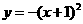

(7)将函数的图象按向量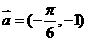平移后所得图象的解析式是

(A) 　　　　(B) 　　　

(C) 　　　　　　　(D)

(8)条件，条件，若p是q的充分不必要条件，则a的取值范围是

(A) 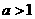　　　(B) 　　　(C) 　　　(D)

(9)已知曲线上一点P到点A(－2，0)、点B(2，0)的距离之差为2，则△PAB是

(A)锐角三角形　　　 (B) 直角三角形　　　 (C)钝角三角形　　　 (D) 等腰三角形

(10)已知过点P(－2，2)且垂直于向量＝(3，4)的直线与圆相切，则实数a的值为

(A) 4　　　 (B) 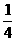　　　　(C) 4或　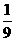　　 (D) －1或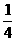

(11)已知集合，则集合A中元素个数为

(A) 16　　　 (B)14　　　 (C)9　　　 (D)8

(12)设数列的前n项和为，令，称为数列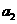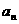，，……，的“理想数”，已知数列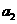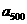，，……，的“理想数”为2004，那么数列2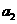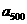， ，，……，的“理想数”为

(A) 2002　　 (B) 2004　　　 (C) 2006　　　 (D) 2008

2004年深圳市高三年级第一次调研考试

数　 学

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　　 球的表面积公式

P(A+B)=P(A)+P(B)　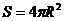　　　　　　　　 其中R表示球的半径

如果事件A、B相互独立，那么　　　　　　　　　　 球的体积公式

P(A·B)=P(A)·P(B)　　　　　　　　　　　　　　 　 其中R表示球的半径

如果事件A在一次试验中发生的概率是P.　 那么n次独立重复试验中恰好发生k次的

概率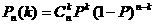

22．函数的定义域为R，且

　 (1)求证：a>0,b<0；

　 (2)若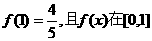上的最小值为，试求f(x)的解析式；

　 (3)在(2)的条件下记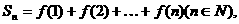试比较

　　　　 的大小并证明你的结论.

21．已知函数f(x)是定义在R上的偶函数，当

　 (1)求当x<0时，f(x)的解析式；

　 (2)试确定函数y=(x≥0)的单调区间，并证明你的结论；

　 (3)若证明：

20．如图，两铁路线垂直相交于站A，若已知AB=100公里，甲火车从A站出发，沿AC方向以50公里/小时的速度行驶，同时乙火车以v公里/小时的速度从B站沿BA方向行驶至A站即停止前行(甲车仍继续行驶).

　 (1)用v表示甲、乙两车的最近距离(两车的车长忽略不计)；

　 　 (2)若甲、乙两车开始行驶到甲、乙两车相距最近时，所用时间为t₀小时，问v为何值时，t₀最大.

19．设数列{a_n}前n的项和为 S_n，且其中m为常数，

　 (1)求证{a_n}是等比数列

　 (2)若数列{a_n}的公比满足q=f(m)且，为等差数列，并求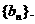

18．平面直角坐标系有点

　 (1)求向量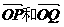的夹角θ的余弦用x表示的函数f(x);

　 (2)求θ的最值.

17．甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ与η，且ξ、η的分布列为：

　 　(1)求a、b的值；

　 (2)甲、乙两名射手在一次射击中的得分均小于3的概率谁更大？

　 (3)计算ξ、η的期望与方差，并以此分析甲乙的技术状况.