
题目列表(包括答案和解析)
2.逻辑联结词的含义,能用“p或q”,“p且q”,“非p”的形式表示复合命题.
1.命题,简单命题,复合命题的概念.
(17)已知集合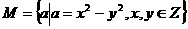 , 若
, 若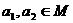 , 试证明
, 试证明 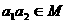 .
.
(18)给定函数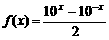 .
.
(Ⅰ)求.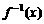 ; (Ⅱ)判断
; (Ⅱ)判断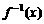 的奇偶性,并证明你的结论.
的奇偶性,并证明你的结论.
(19)已知函数f(x)=a+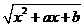 (a,b为实常数)
(a,b为实常数)
(I) 若a=2,b=-1,求f(x)的值域.
(II) 若f(x)的值域为[0,+∞),求常数a,b应满足的条件.
(20)某校校长暑假将带领该校市级“三好生”去北京旅游。甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优待。”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠。”若全票价为240元.
(I)设学生数为x,甲旅行社收费为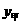 ,乙旅行社收费为
,乙旅行社收费为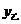 ,分别计算两家旅行社的收费(建立表达式);
,分别计算两家旅行社的收费(建立表达式);
(II)当学生数是多少时,两家旅行社的收费一样;
(III)就学生数x讨论哪家旅行社更优惠.
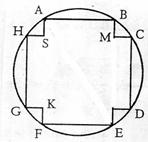
(21)有一种变压器,铁芯的截面是正十字形(如图(5)),其中矩形ABEF与矩形CDGH全等,且AS=KF=HS=MC,为保证所需的磁通量,要求正十字形面积为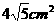 ,为了使绕铁芯的铜线最省,即正十字形外接圆周长最小,正十字形的AB、BE长度应各为多少cm?
,为了使绕铁芯的铜线最省,即正十字形外接圆周长最小,正十字形的AB、BE长度应各为多少cm?
(22) 定义在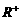 上的函数f(x),对于任意的
上的函数f(x),对于任意的 ,都有
,都有 成立,当
成立,当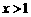 时,
时,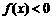 .
.
(Ⅰ)计算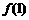 ;
;
(Ⅱ)证明f (x)在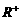 上是减函数;
上是减函数;
(Ⅲ)当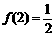 时,解不等式
时,解不等式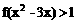 .
.
(13)函数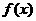 的图象与
的图象与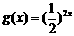 的图象关于直线y=x对称,则
的图象关于直线y=x对称,则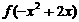 的递减区间是
.
的递减区间是
.
(14)已知函数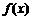 是奇函数,当
是奇函数,当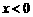 时,
时,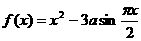 ,且
,且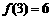 ,则a等于 .
,则a等于 .
(15)函数f(x)满足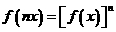 写出一个满足上述条件的函数_______.
写出一个满足上述条件的函数_______.
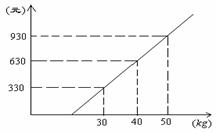 (16)某航空公司规定,乘机所携带行李的重量(kg)与其运费(元)由如图的一次函数图像确定,那么乘客免费可携带行李的最大重量为 ______ ______.
(16)某航空公司规定,乘机所携带行李的重量(kg)与其运费(元)由如图的一次函数图像确定,那么乘客免费可携带行李的最大重量为 ______ ______.
(1)已知集合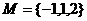 ,集合
,集合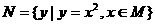 ,则
,则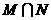 是 ( )
是 ( )
(A) 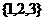 (B)
(B) 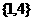 (C)
(C) 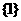 (D)
(D) 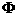
(2) a、b为实数,集合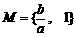 ,
,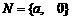 ,
,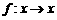 表示把集合M中的元素
表示把集合M中的元素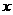 映射到集合N中仍为
映射到集合N中仍为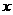 ,则a+b ( )
,则a+b ( )
(A)
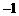 (B) 0
(C) 1
(D)
(B) 0
(C) 1
(D) 
(3)已知函数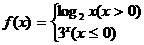 ,那么
,那么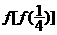 的值为
( )
的值为
( )
(A)9
(B)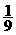 (C)-9 (D)
(C)-9 (D)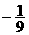
(4)设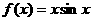 ,若
,若 、
、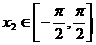 且
且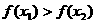 ,则下列不等式必定成立的是
( )
,则下列不等式必定成立的是
( )
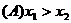 (B)
(B)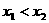 (C)
(C)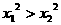 (D)
(D)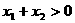
(5)函数 y=-x(x+2)(x≥0)的反函数定义域为 ( ) (A)
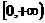 (B)
(B)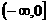
(C)
(0,1) (D)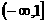
(6)设函数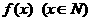 表示
表示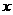 除以3的余数,对
除以3的余数,对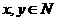 都有
( )
都有
( )
(A) 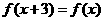 (B)
(B)
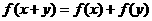
(C) 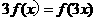 (D)
(D)
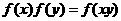
(7)函数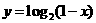 的图象是
( )
的图象是
( )
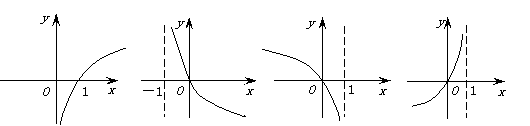 (A)
(B) (C)
(D)
(A)
(B) (C)
(D)
(8)设函数f (x)=ax2+bx+c对任意实数t都有f (2+t)= f (2-t)成立,在函数值f (-1),f (1),f (2),f (5)中的最小的一个不可能是 ( )
(A) f (-1) (B) f (1) (C) f (2) (D) f (5)
(9)已知函数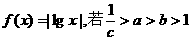 ,则 ( )
,则 ( )
(A) 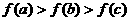 (B)
(B) 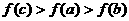
(C) 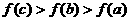 (D)
(D) 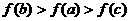
(10)由等式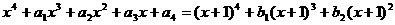
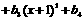 定义
定义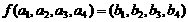 ,则
,则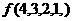 等于 ( )
等于 ( )
( )
)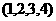 (
( )
)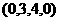
(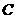 )
) (
(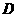 )
)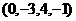
(11)若方程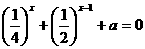 有正数解,则实数
有正数解,则实数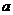 的取值范围是 ( )
的取值范围是 ( )
(A) (B)
(B)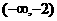
(C)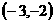 (D)
(D)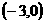
(12)二次函数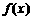 满足
满足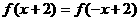 , 又
, 又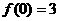 ,
, .若在
.若在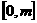 有最大值3, 最小值1, 则
有最大值3, 最小值1, 则 的取值范围是 ( )
的取值范围是 ( )
(A)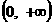 (B)
(B)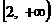
(C)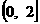 (D)
(D)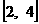
9.某工厂有旧墙一面长14米,现准备利用这面旧墙建造平面图形为矩形,面积为126米2的厂房,工程条件是:①建1米新墙的费用为a元;②修1米旧墙的费用是a/4元;③拆去1米旧墙用所得的材料建1米新墙的费用为a/2元. 经过讨论有两种方案:
(1) 利用旧墙的一段x米(x<14)为矩形厂房的一面边长;
(2) 矩形厂房的一面边长x≥14.
问如何利用旧墙,即x为多少时建墙费用最省?(1)(2)两种方案哪种方案最好?
8.为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元.若总用电量为S千瓦时,设高峰时段用电量为X千瓦时.
(1)写出实行峰谷电价的电费y1=g1(x)及现行电价的电费y2=g2(S)的函数解析式及电费总差额f(x)=y2-y1的解析式;
(2)对于用电量按时均等的电器(在任何相同的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?
(3)若每户实行“峰谷电价”的居民需缴纳安装“分时段电能计量表”的成本费100元.在用电量按时均等的条件下,一户居民要在一年内收回安装“分时段电能计量表”的成本费,每户每月用电至少要不低于多少千瓦时(结果取整数)?
7.某工厂最近用50万元购买一台德国仿型铣床,在买回来以后的第二天投入使用,使用后的第t天应付的保养费是(t + 500)元,(买来当天的保养维修费以t = 0计算),机器从买来当天到报废共付的保养维修费与购买机器费用的和平均摊到每一天的费用叫做每天的平均损耗.当平均损耗达到最小值时,机器报废最划算.
(1) 求每天平均损耗y (元)表示为天数x的函数;
(2) 求该机器买回来后多少天应报废.
6.长江三峡大江截流工程有关数据如下表所示:
|
时 间 |
9:00 |
10:00 |
12:00 |
… |
16:00 |
|
龙口宽 |
40m |
39m |
34m |
… |
|
|
工程进展 |
|
1m |
5m |
… |
|
|
模拟数列 |
|
a1 |
a2+a3 |
… |
a7 |
预计16:00合龙.
(1)同学甲将工程进展情况模拟成等差数列,即a1=1,a2+a3=5,根据表中所列数据,通过计算,说明能否按期合龙.
(2)同学乙将工程进展情况模拟成等比数列,根据表中所列数据,通过计算,说明能否合龙(取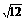 =4.6).
=4.6).
5.甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数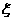 的数学期望和方差.
的数学期望和方差.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com