
题目列表(包括答案和解析)
9.函数y=f(x)和函数y=g(x)的图象如下图所示,则y=f(x)·g(x)的图象可能是(A)
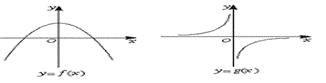
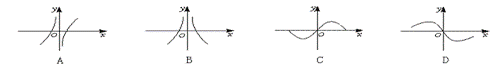
8.抛物线的焦点是(2,1),准线方程是x+y+1=0,则抛物线的顶点是(B)
A.(0,0) B.(1,0) C.(0, -1) D.(1,1)
7.在椭圆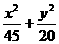 =1上有一点P,F1、F2是椭圆的左右焦点,△F1PF2为直角三角形,则这样的点P有(D)
=1上有一点P,F1、F2是椭圆的左右焦点,△F1PF2为直角三角形,则这样的点P有(D)
A.2个 B.4个 C.6个 D.8个
6.椭圆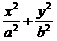 =1(a>b>0)的四个顶点为A、B、C、D,若菱形ABCD的内切圆恰好过焦点,则椭圆的离心率是(D)
=1(a>b>0)的四个顶点为A、B、C、D,若菱形ABCD的内切圆恰好过焦点,则椭圆的离心率是(D)
A.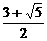 B.
B. 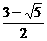 C.
C. 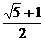 D.
D.
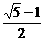
依题意c=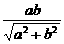 即c2(a2+b2)=a2b2又b2=a2-c2故c4-3a2c2+a4=0
即c2(a2+b2)=a2b2又b2=a2-c2故c4-3a2c2+a4=0
即(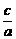 )4-3(
)4-3(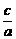 )2+1=0故e2=(
)2+1=0故e2=(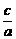 )2=
)2=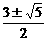 (舍正),e=
(舍正),e=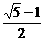
5.异面直线a、b成80°角,P为a、b外一定点,若过P有且仅有2条直线与a、b所成角都为θ,则θ∈(B)
A.{θ|0°<θ<40°} B.{θ|40°<θ<50°}
C.{θ|40°<θ<90°} D.{θ|50°<θ<90°}
4.k∈R,直线(k+1)x-ky-1=0被圆(x-1)2+(y-1)2=4截得的弦长是(C)
A.8 B.2 C.4 D.值与k有关
3.函数y=1+3x-x3有(D)
A.极小值-1,极大值1 B.极小值-2,极大值3
C.极小值-2,极大值2 D.极小值-1,极大值3
2.已知数列{an}的前n项和Sn=an-1(a∈R,a≠0),则{an}(C)
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列,或者是等比数列 D.等差、等比数列都不是
1.已知直线l、m,平面α、β,且l⊥α,m β.给出下列四个命题:(1)若α∥β,则l⊥m;(2)若l⊥m,则α∥β;(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β
β.给出下列四个命题:(1)若α∥β,则l⊥m;(2)若l⊥m,则α∥β;(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β
其中正确的命题个数是(D)
A.4 B.1 C.3 D.2
22.(本小题满分14分)
已知函数f(x-2)=ax2-(a-3)x+a-2(a<0,a∈Z)的图象与x轴有交点.
(1)求a的值;(2)求f(x)的解析式;
(3)若g(x)=1-[f(x)]2,F(x)=c·g(x)+d·f(x),问是否存在c(c>0),d使得在区间(-∞,f(2))内是单调递增函数,而在区间(f(2),0)内是单调递减函数?若存在,求c,d之间的关系,并写出推理过程;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com