
题目列表(包括答案和解析)
2、函数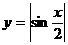 的最小正周期是( )
的最小正周期是( )
A、 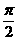 B、
B、 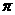 C、
C、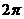 D、
D、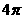
1、设集合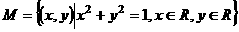 ,
,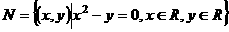 ,则集合
,则集合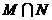 中元素的个数为( )
中元素的个数为( )
A、1 B、2 C、3 D、4
已知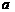 为第二象限的角,
为第二象限的角,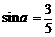 ,
,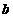 为第一象限的角,
为第一象限的角,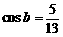 .求
.求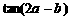 的值.
的值.
甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响,求
(Ⅰ) 前三局比赛甲队领先的概率;
(Ⅱ) 本场比赛乙队以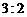 取胜的概率.
取胜的概率.
(精确到0.001)
已知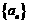 是各项为不同的正数的等差数列,
是各项为不同的正数的等差数列,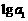 、
、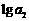 、
、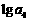 成等差数列.又
成等差数列.又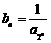 ,
,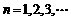 .
.
(Ⅰ) 证明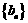 为等比数列;
为等比数列;
(Ⅱ) 如果数列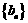 前3项的和等于
前3项的和等于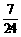 ,求数列
,求数列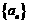 的首项
的首项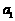 和公差
和公差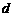 .
.
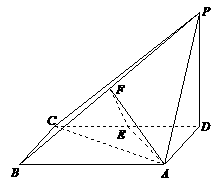
如图,四棱锥 中,底面
中,底面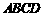 为矩形,
为矩形,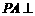 底面
底面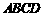 ,
,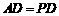 ,
,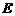 、
、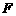 分别为
分别为 、
、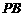 的中点.
的中点.
(Ⅰ) 求证: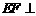 ⊥平面
⊥平面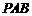 ;
;
(Ⅱ) 设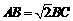 ,求
,求 与平面
与平面 所成的角的大小.
所成的角的大小.
设 为实数,函数
为实数,函数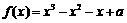 .
.
(Ⅰ) 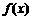 的极值;
的极值;
(Ⅱ) 当 在什么范围内取值时,曲线
在什么范围内取值时,曲线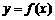 与
与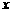 轴仅有一个交点.
轴仅有一个交点.
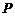 、
、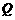 、
、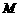 、
、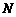 四点都在椭圆
四点都在椭圆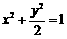 上,
上,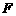 为椭圆在
为椭圆在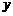 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知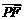 与
与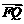 共线,
共线,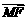 与
与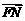 共线,且
共线,且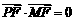 .求四边形
.求四边形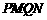 的面积的最小值和最大值.
的面积的最小值和最大值.
(1)
函数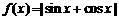 的最小正周期是
的最小正周期是
(A) 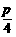 (B)
(B)
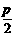 (C)
(C)
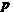 (D)
(D)
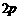
(2)
正方体 中,
中,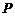 、
、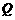 、
、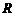 分别是
分别是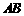 、
、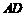 、
、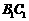 的中点.那么,正方体的过
的中点.那么,正方体的过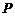 、
、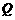 、
、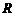 的截面图形是
的截面图形是
(A) 三角形 (B) 四边形 (C) 五边形 (D) 六边形
(3)
函数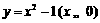 的反函数是
的反函数是
(A) 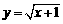
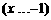 (B)
(B)
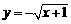
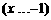
(C) 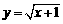
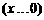 (D)
(D)
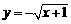
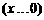
(4)
已知函数 在
在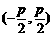 内是减函数,则
内是减函数,则
(A) 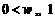 (B)
(B)
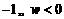 (C)
(C)
 (D)
(D)

(5)
抛物线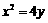 上一点
上一点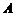 的纵坐标为4,则点
的纵坐标为4,则点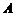 与抛物线焦点的距离为
与抛物线焦点的距离为
(A) 2 (B) 3 (C) 4 (D) 5
(6)
双曲线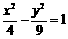 的渐近线方程是
的渐近线方程是
(A) 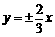 (B)
(B)
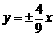 (C)
(C)
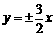 (D)
(D)

(7)
如果数列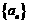 是等差数列,则
是等差数列,则
(A)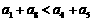 (B)
(B)
 (C)
(C) 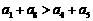 (D)
(D) 
(8)
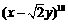 的展开式中
的展开式中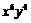 项的系数是
项的系数是
(A) 840 (B)
 (C)
210 (D)
(C)
210 (D)
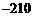
(9)
已知点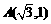 ,
,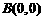 ,
,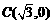 .设
.设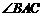 的一平分线
的一平分线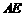 与
与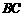 相交于
相交于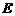 ,那么有
,那么有 ,其中
,其中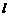 等于
等于
(A) 2 (B)
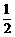 (C)
(C)
 (D)
(D)
(10) 已知集合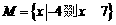 ,
,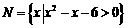 ,则
,则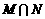 为
为
(A) 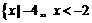 或
或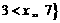 (B)
(B)
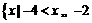 或
或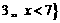
(C) 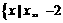 或
或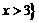 (D)
(D)
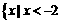 或
或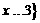
(11) 点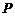 在平面上作匀速直线运动,速度向量
在平面上作匀速直线运动,速度向量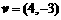 (即点
(即点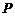 的运动方向与
的运动方向与 相同,且每秒移动的距离为
相同,且每秒移动的距离为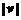 个单位).设开始时点
个单位).设开始时点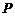 的坐标为
的坐标为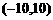 ,则5秒后点
,则5秒后点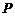 的坐标为
的坐标为
(A) 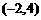 (B)
(B)
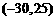 (C)
(C)
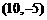 (D)
(D)
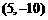
(12) △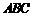 的顶点
的顶点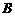 在平面
在平面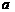 内,
内,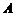 、
、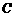 在
在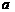 的同一侧,
的同一侧,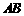 、
、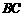 与
与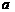 所成的角分别是
所成的角分别是 和
和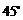 .若
.若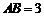 ,
,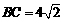 ,
,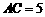 ,则
,则 与
与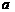 所成的角为
所成的角为
(A) 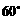 (B)
(B)
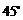 (C)
(C)
 (D)
(D)
普通高等学校全国统一考试
文科数学(必修+选修Ⅰ)
第Ⅱ卷
(13) 在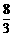 和
和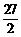 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为____________.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积为____________.
(14) 圆心为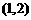 且与直线
且与直线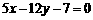 相切的圆的方程为_____________________.
相切的圆的方程为_____________________.
(15) 在由数字0, 1, 2, 3, 4, 5所组成的没有重复数字的四位数中,不能被5整除的数共有_____________个.
(16) 下面是关于三棱锥的四个命题:
① 底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
② 底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
③ 底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④ 侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中,真命题的编号是______________.(写出所有真命题的编号)
22.(本小题满分14分)
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点;
(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围;
(3)求证:当x≤-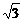 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).
21.(本小题满分12分)
某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建设面积为1000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该球场建x个时,每平方米的平均建设费用用f(x)表示,且f(n)=f(m)(1+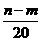 )(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
)(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
20.(本小题满分12分)
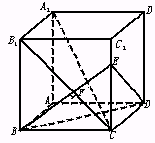 已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
(1)求证A1C⊥平面EBD;
(2)求点A到平面A1B1C的距离;
(3)求平面A1B1C与平面BDE所成角的度数;
(4)求ED与平面A1B1C1所成角的大小;
19.(本小题满分12分)
已知平面向量a=(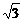 ,-1),b=(
,-1),b=(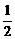 ,
,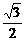 ).
).
(1)证明:a⊥b;
(2)若存在实数k和t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)根据(2)的结论,确定k=f(t)的单调区间.
18. (本小题满分12分)
在数列{an}中,a1=1,a2=3,且an+1=4an-3an-1,求an.
17.(12分)已知关于x的方程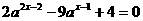 有一根是2.
有一根是2.
(1)求实数a的值;(2)若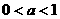 ,求不等式
,求不等式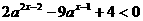 的解集.
的解集.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com