
题目列表(包括答案和解析)
5.已知A、B、C、D是坐标平面上不共线的四点,则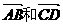 共线是
共线是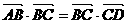 =0
=0
的什么条件 (B)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.椭圆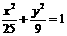 的焦点为F1和F2,点P在椭圆上,若线段PF1的中点在y轴上,那么
的焦点为F1和F2,点P在椭圆上,若线段PF1的中点在y轴上,那么
|PF1| : |PF2|的值为 (B)
A.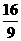 B.
B.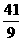 C.
C.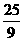 D.
D.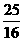
3.若过球面上A、B、C三点的截面与球心的距离恰为球半径的一半,且AB=BC=CA=2,
则球体积为 (D)
A.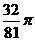 B.
B.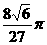 C.
C.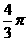 D.
D.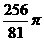
2.设函数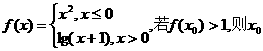 的取值范围为 (D)
的取值范围为 (D)
A.(-1,1) B.(-1,+∞) C.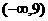 D.
D.
1.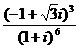 的值为 (B)
的值为 (B)
A.1 B.i C.-i D.-1
22.(本小题满分14分)
已知函数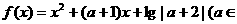 R,且
R,且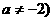 .
.
(I)若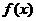 能表示成一个奇函数
能表示成一个奇函数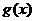 和一个偶函数
和一个偶函数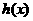 的和,求
的和,求 的解析
的解析
式;
(II)命题P:函数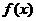 在区间
在区间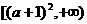 上是增函数;
上是增函数;
命题Q:函数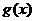 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较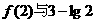 的大小.
的大小.
解:(1)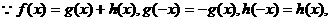
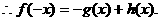
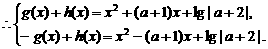 ………2分
………2分
解得 ………………4分
………………4分
(2)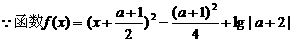 在区间
在区间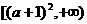 上是增函数,
上是增函数,
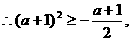 解得
解得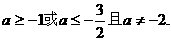 …………6分
…………6分
又由函数 是减函数,得
是减函数,得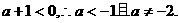 …………8分
…………8分
∴命题P为真的条件是: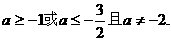
命题Q为真的条件是: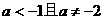 .
.
又∵命题P、Q有且仅有一个是真命题,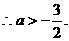 ……………………10分
……………………10分
(2)由(1)得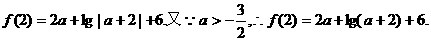
设函数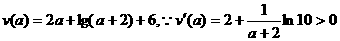 .
.
∴函数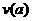 在区间
在区间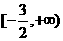 上为增函数.………………12分
上为增函数.………………12分
又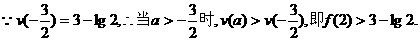 ………14分
………14分
21.(本小题满分12分)
已知点H(-6,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足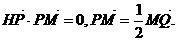
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-2,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点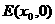 ,
,
使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
解(1)设点M的坐标为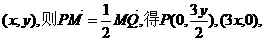
由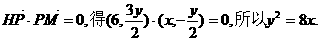
由点Q在x轴的正半轴上,得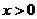 .
.
所以,动点M的轨迹C是以(0,0)为顶点,以(2,0)为焦点的抛物线,除去原点.
(2)设直线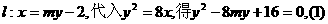

设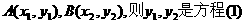 的两个实数根,由韦达定理得
的两个实数根,由韦达定理得
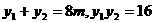 ,
,
所以,线段AB的中点坐标为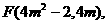
而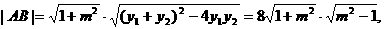
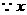 轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,
轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,
∴点F到x轴的距离不大于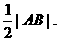
所以 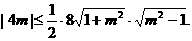
化简得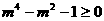 ,解之得
,解之得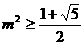 ,结合(*)得
,结合(*)得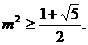
又因为直线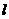 的斜率
的斜率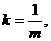 所以
所以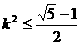 ,显然
,显然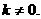
故所求直线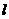 的斜率k的取值范围为
的斜率k的取值范围为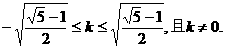
20.(本小题满分12分)
设数列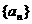 是等比数列,
是等比数列,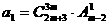 ,公比q是
,公比q是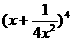 的展开式中的第二项
的展开式中的第二项
(按x的降幂排列).
(1)用n,x表示通项an与前n项和Sn;
(2)若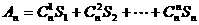 ,用n,x表示An.
,用n,x表示An.
解(1)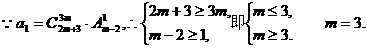
由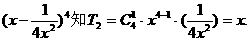
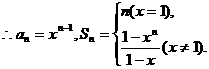
(2)当x=1时,Sn=n,
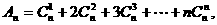
又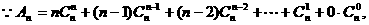
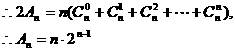
当
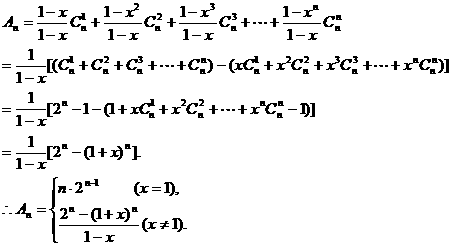
19.(本小题满分12分)
为了测试甲、乙两名射击运动员的射击水平,让他们各向目标靶射出10次,其中甲击中目标7次,乙击中目标6次,若再让甲、乙两人各自向目标靶射击3次,求:
(1)甲运动员恰好击中目标2次的概率是多少?
(2)两名运动员都恰好击中目标2次的概率是多少?(结果保留两个有效数字).
:依题意,知
甲运动员向目标靶射击1次,击中目标的概率为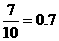 ;
;
乙运动员向目标靶射击1次,击中目标的概率为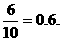
(1)甲运动员向目标靶射击3次,恰好击中目标2次的概率是
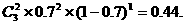
(2)甲、乙两运动员各自向目标靶射击3次,恰好都击中目标2次的概率是
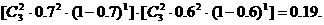
18.(本小题满分12分)
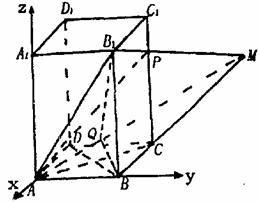
在正四棱柱ABCD-A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线.
解(1)由题意可知,不论P点在棱CC1上的任何位置,AP在底面ABCD内射影都是
AC, 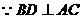 ,
, 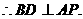
(2)延长B1P和BC,设B1P∩BC=M,连结AM,则AM=平面AB1P∩平面ABCD. 过B作BQ⊥AM于Q,连结B1Q,由于BQ是B1;Q在底面ABCD内的射影,所以B1Q⊥AM,故∠B1QB就是所求二面角的平面角,依题意,知CM=2B1C1,从而BM=3BC. 所以
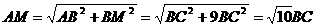 . 在
. 在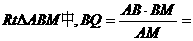
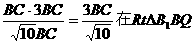 中,
中,
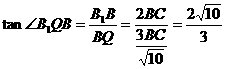 ,
,
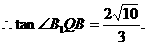
 得
得

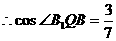 为所求.
为所求.
(3)设CP=a,BC=m,则BB1=2m,C1P=2m-a,从而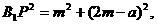
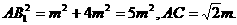
在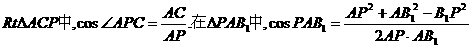
依题意,得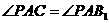 .
.  .
.
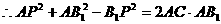 .
.
即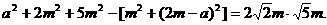
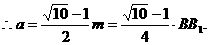
故P距C点的距离是侧棱的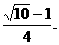
别解:如图,建立空间直角坐标系.
设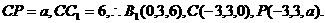
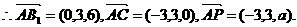
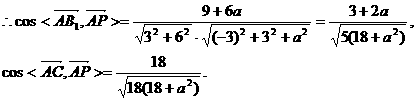
依题意,得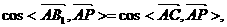
即
故P距C点的距离是侧棱的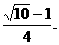
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com