21.(本小题满分12分)

设f(x)=ax²+bx+c(a＞b＞c),f(1)=0,g(x)=ax+b.

(1)求证：函数y=f(x)与y=g(x)的图象有两个交点；

(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A₁、B₁，求｜A₁B₁｜的取值范围；

(3)求证：当x≤－时，恒有f(x)＞g(x).

20.(本小题满分12分)

直线l：y=mx+1与椭圆C：ax²+y²=2交于A、B两点，以OA、OB为邻边作平行四边形OAPB(O为坐标原点)

(1)当a=2时，求点P的轨迹方程；

(2)当a,m满足a+2m²=1，且记平行四边形OAPB的面积函数S(a),求证：2＜S(a)＜4.

19.(本小题满分12分)

　市场营销人员对过去几年某产品的价格及销售数量的关系做数据分析，有如下的规律，该商品的价格每上涨x%(x＞0),销售量就减少kx%(其中k为正常数)，目前该商品定价为a元，统计其销售量为b个.

(1)当k=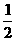时，该商品的价格上涨多少，就能使销售的总金额达到最大？

(2)在适当的涨价过程中，求使销售总金额不断增加时，k的取值范围.

18.如图，四棱锥P-ABCD中，PD⊥平面ABCD，PA与平面

ABCD所成的角为60°,在四边形ABCD中，∠D=∠DAB=90°，

AB=4，CD=1，AD=2.

　　　 (Ⅰ)建立适当的坐标系，并写出点B、P的坐标；

　　　 (Ⅱ)求异面直线PA与BC所成的角；

　　　 (Ⅲ)若PA的中点为M，求证：平面AMC⊥平面PBC.

17.(本小题满分12分)

甲、乙两个乒乓球运动员进行乒乓球单打比赛，已知在一局比赛中甲获胜的概率为0.6，乙获胜的概率为0.4，比赛时可以用三局两胜或五局三胜制，问在哪一种比赛制度下甲获胜的可能性较大？

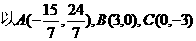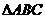16．为顶点的与圆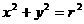(r>0)没有公共点，则

圆的半径r的取值范围：

15.已知函数f(x)满足：f(p+q)=f(p)f(q),f(1)=3,则

=_______________.

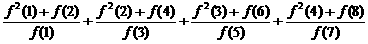14.若抛物线上的各点与焦点距离最小值是2，则过焦点与抛物线的对称轴成角的弦长是：

13.设f(x)=x²+x+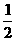的定义域是［n,n+1］(n∈N^*),则函数f(x)的值域中含有的整数的个数为：

12.△ABC中，AB=9，AC=15，∠BAC=120°，△ABC所在平面外一点P到三个顶点A、B、C的距离都是14，那么点P到平面α的距离为(　 )

A.7　　　　　　　　　　　　　　　　　　 B.9　 　　　　　　　　　　　　　　 C.11　　　　　　　　　　　 D.13