
题目列表(包括答案和解析)
22.(本小题满分14分)已知 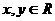 ,
,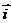 、
、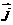 为直角坐标平面内
为直角坐标平面内 、
、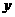 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量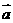 =
=
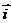 +(
+(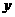 +2)
+2)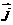 ,
, 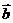 =
=
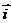 +(
+(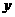 -2)
-2)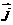 ,且
,且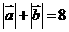 .
.
(1)求点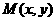 的轨迹C的方程;
的轨迹C的方程;
(2)过点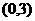 作直线
作直线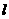 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设 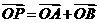 ,是否存在这样的直线
,是否存在这样的直线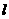 ,使得四边形OAPB是矩形?若存在,求出直线
,使得四边形OAPB是矩形?若存在,求出直线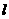 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
21.(本小题满分12分)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为 个,零件的实际出厂单价为P元,写出函数
个,零件的实际出厂单价为P元,写出函数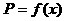 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
20.(本小题满分12分)对于任意实数 ,符号
,符号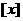 表示
表示
的整数部分,即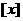 是不超过
是不超过 的最大整数.在实数轴(箭头向右)上
的最大整数.在实数轴(箭头向右)上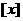 是在点
是在点 左侧的第一个整数点,当
左侧的第一个整数点,当 是整数时
是整数时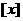 就是
就是 .这个函数
.这个函数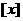 叫做“取整函数”也叫高斯(Gauss)函数.
叫做“取整函数”也叫高斯(Gauss)函数.
从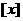 的定义可得下列性质:
的定义可得下列性质: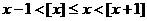 .
.
与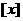 有关的另一个函数是
有关的另一个函数是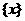 ,它的定义是
,它的定义是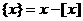 ,
,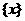 称为
称为 的“小数部分”.
的“小数部分”.
(1)根据上文可知,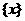 的取值范围是____________,
的取值范围是____________,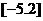 =_____________;
=_____________;
(2)求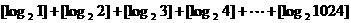 的和.
的和.
19.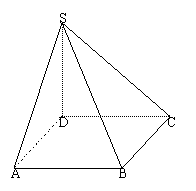 (本小题满分12分)如图,四棱锥
(本小题满分12分)如图,四棱锥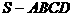 的底面
的底面
是边长为1的正方形,SD垂直于底面ABCD,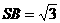 .
.
(1)求证: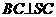 ;
;
(2)求平面ASD与平面BSC所成二面角的大小;
(3)设棱SA的中点为M,求异面直线DM与SB所成角
的大小.
18.(本小题满分12分)在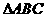 中,
中,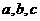 分别是
分别是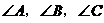 的对边长,已知
的对边长,已知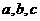 成等比数列,且
成等比数列,且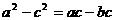 ,求
,求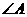 的大小及
的大小及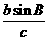 的值.
的值.
0.6,0.7,0.8,求元件连接成的系统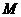 正常
正常
工作的概率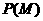 .
.
17.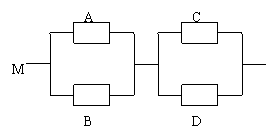 (本小题满分12分)如图,用
(本小题满分12分)如图,用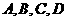 表示四类不同的元件连接成系统
表示四类不同的元件连接成系统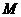 .当元件
.当元件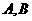 至少有一个正常工作且元件
至少有一个正常工作且元件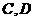 至少
至少
有一个正常工作时,系统 正常工作.已知
正常工作.已知
元件 正常工作的概率依次为0.5,
正常工作的概率依次为0.5,
16.一水池有2个进水口,1 个出水口,进出水速度如图甲、乙所示. 某天0点到6点,
该水池的蓄水量如图丙所示.(至少打开一个水口)
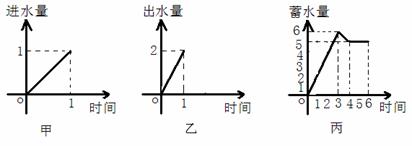
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断序号是_______________.
15.过点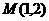 的直线
的直线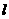 将圆:
将圆: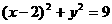 分成两段弧,当其中的劣弧最短时,直线
分成两段弧,当其中的劣弧最短时,直线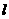 的方程为 __________
.
的方程为 __________
.
14.正三棱锥的顶点都在同一个半径为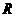 的球面上,球
的球面上,球
心到该棱锥底面的距离是球半径的一半,则该棱锥的体
积是____________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com