
题目列表(包括答案和解析)
第二轮复习侧重的应是解题能力的培养,尤其是读题能力、类比能力和转化能力;对于立体几何的能力培养,我认为应从以下几方面着手:
1、重视已知条件与图形的对号入座
 解立几题一般需作好两个图,一是立体图,把已知条件中的线段长、角度值在图中标出,对于图形翻折、旋转等问题把折前及折后的长度、角度对应起来,往往发现解题思路或部分结论。二是用来计算的铅垂放置的平面图(解题关键图),利于正确运算。
解立几题一般需作好两个图,一是立体图,把已知条件中的线段长、角度值在图中标出,对于图形翻折、旋转等问题把折前及折后的长度、角度对应起来,往往发现解题思路或部分结论。二是用来计算的铅垂放置的平面图(解题关键图),利于正确运算。
[例6](2003汕头一模)已知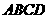 是矩形,
是矩形,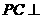 平面
平面
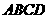 ,
,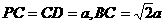 ,
, 分别是
分别是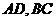
的中点;(1)求证:二面角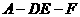 是直二面角;
是直二面角;
(2)求点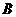 到平面
到平面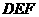 的距离。
的距离。
简析:依次标出已知条件得到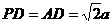 ,
,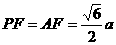 ,所以
,所以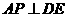 ,
,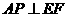 ,从而(1)得到证明,(2)也可利用
,从而(1)得到证明,(2)也可利用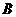 到平面
到平面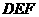 的距离为
的距离为 到平面
到平面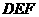 的距离的一半得以很快解决。
的距离的一半得以很快解决。
3、利用平面的法向量求解角和距离问题
当作平面的垂线难度较大时,可利用平面的法向量求解一些角和距离问题。如图,平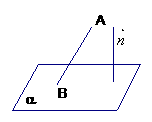 面
面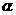 的法向量为
的法向量为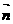 ,
,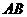 为平面
为平面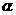 的斜线,
的斜线,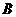 为斜足,则
为斜足,则
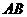 与平面
与平面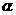 所成的角
所成的角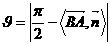 ;用向量在法向量
;用向量在法向量
上的投影公式易得:点 到平面
到平面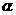 的距离
的距离
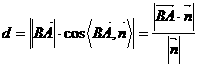 ;当
;当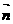 与异面直线
与异面直线 ,
,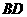 都垂直时,
都垂直时,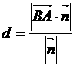 为异面直线
为异面直线 ,
,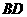 的距离公式。设二面角
的距离公式。设二面角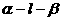 ,
,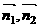 分别为平面
分别为平面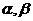 的法向量,则二面角
的法向量,则二面角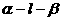 的大小为
的大小为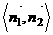 或它的补角。
或它的补角。
 [例5](教材习题)棱长为1的正方体
[例5](教材习题)棱长为1的正方体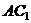 中,
中,
求面对角线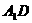 和
和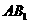 的距离。
的距离。
解:建立如图直角坐标系,则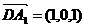
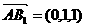 ,设
,设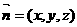 ,由
,由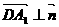 ,
,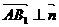
得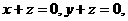 令
令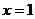 ,则
,则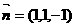 ,又
,又
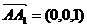 ,所以
,所以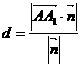
 。
。
2、利用空间向量解探索性问题
对于立几中的探索性问题及存在性问题,用“形”解难度很大,而“数”中的待定系数法正好运用。
 [例3](2000全国节选)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°。
[例3](2000全国节选)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°。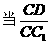 的值
的值
为多大时,能够使A1C⊥平面C1BD ? 请给出证明。
解:设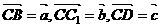 ,
,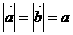
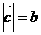 ,则
,则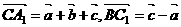 ,
,
当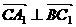 时
时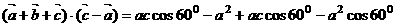
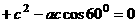 ,解得
,解得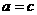 ,所以
,所以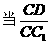 =1时A1C⊥平面C1BD。
=1时A1C⊥平面C1BD。
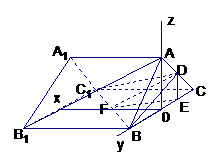 [例4](94全国节选)如图,已知
[例4](94全国节选)如图,已知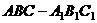 是正三棱柱,
是正三棱柱,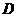 是
是 的中点,
的中点,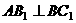 ,求二面角
,求二面角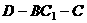 的度数。
的度数。
简析:此题学生很易作出二面角的平面角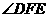 ,
,
但用传统方法难以求出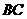 与
与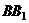 的长度关系;
的长度关系;
若用向量解:在如图坐标系下,设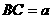 ,
,
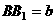 则
则 ,
,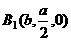 ,
,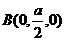 ,
,
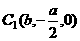 ,
,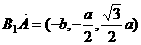
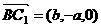 ,
,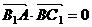 得,
得,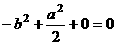 ,
,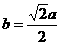 ,很快得出结论。
,很快得出结论。
利用空间向量解立几题,体现了空间的数形结合思想,顺应了几何改革代数化的方向;利用空间向量解立几题,首先应是确定基向量。即 或单位正交基底
或单位正交基底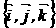 。
。
1、利用空间向量解线线平行、垂直问题
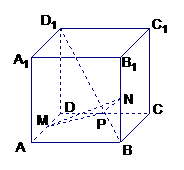 [例1](2003全国节选)正方体
[例1](2003全国节选)正方体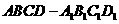 中,
中,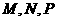 分别为
分别为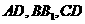 的中点,证明:
的中点,证明: 与平面
与平面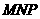 不垂直。
不垂直。
分析:用传统方法证明 与
与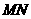 不垂直,有难度;
不垂直,有难度;
利用向量: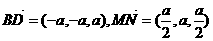 ,
,
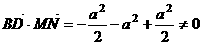 ,所以
,所以 与
与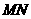 不垂直。
不垂直。
[例2](2003全国)如图,直三棱柱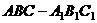 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,
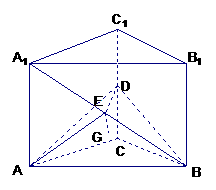
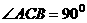 ,侧棱
,侧棱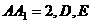 分别是CC1与A1B的
分别是CC1与A1B的
中点,点E在平面ABD上的射影是△ABD的重心G。
(1)求A1B与平面ABD所成角的大小(结果用反三
角函数值表示);
(2)求点A1到平面AED的距离.
简析:传统解法解此题难点一是重心G的运用,而用向
量解:由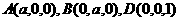 很快得
很快得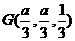 ,
,
二是如何由条件求出 的长,应用向量则由
的长,应用向量则由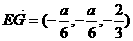 与
与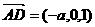 垂直易得
垂直易得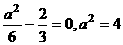 。
。
新教材立体几何内容变化较大,主要是删去了棱台、旋转体、球冠、多面体及旋转体体积等;增加了正多面体的概念,多面体的欧拉公式,最大变化是首次引入空间向量,并用这一工具去解决空间直线的平行、垂直关系,以及求空间的“距离”、“角”。从近几年的高考题来看,新教材的甲组题(即9B考题)比乙组题(即9A考题)和全国题都容易做。还有用向量方法去解部分传统的立体几何题也是有优势的,如2000、2003年全国高考立体几何题,普遍都认为较难,但如果用向量方法去解,就很简单了。因此,要重点掌握“空间向量”,并突出其“工具性”。
22.(本小题满分14分)
已知A、B是椭圆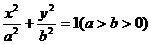 的一条弦,向量
的一条弦,向量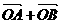 与AB交于M,且
与AB交于M,且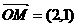 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线AB交于N(4,-1).
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线AB交于N(4,-1).
(1)求椭圆的离心率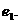 ;
;
(2)设双曲线的离心率为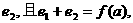 求
求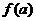 的解析式,并求它的定义域和值域.
的解析式,并求它的定义域和值域.
21、(本小题满分12分)
设函数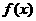 与数列
与数列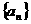 满足关系:
满足关系:
①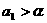 ,其中
,其中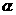 是方程
是方程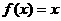 的实数根;
的实数根;
 ②
②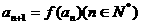 ;
;
③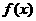 的导数
的导数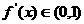 。
。
(Ⅰ) 证明: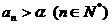 ;
;
(Ⅱ) 判断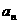 与
与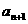 的大小,并证明你的结论。
的大小,并证明你的结论。
|
20、(本小题满分12分)
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分。已知射手甲在100m处击中目标的概率为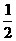 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(Ⅰ) 求这名射手在三次射击中命中目标的概率;
(Ⅱ) 求这位射手在这次射击比赛中得分的数学期望.
19、(本小题满分12分)
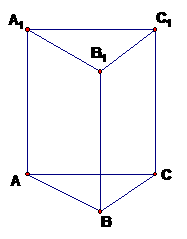 如图所示,已知正三棱柱
如图所示,已知正三棱柱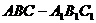 的底面边长为1,若点M在侧棱
的底面边长为1,若点M在侧棱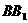 上,且AM与侧面
上,且AM与侧面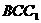 所成的角为
所成的角为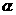 ;
;
(Ⅰ)若BM=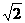 ,求
,求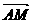 与
与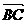 所成的角;
所成的角;
(Ⅱ)判断棱柱的高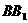 等于多少时能使得
等于多少时能使得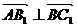 ? 请给出证明.
? 请给出证明.
|
18、(本小题满分12分)
已知条件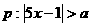 和条件
和条件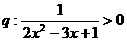 ,请选取适当的实数
,请选取适当的实数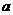 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题。则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题。
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题。则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com