
题目列表(包括答案和解析)
6.2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有 .
5.已知f(x)是一次函数,f(10)=21,且f(2), f(7),f(22)成等比数列,则f(1)+f(2)+…… +f(n)等于 .
4.正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为 ,则这个棱柱的侧面对角线
,则这个棱柱的侧面对角线
E1D与BC1所成的角是 .
3.在(1-x)5(1+x)4的展开式中x3的系数是 .
2.若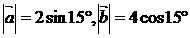 ,
, 的夹角为30°,则
的夹角为30°,则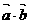 的值为 .
的值为 .
1.x∈R时,函数y=3sin(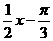 )的周期是 .
)的周期是 .
22.(I)由函数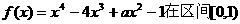 单调递增,在区间
单调递增,在区间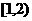 单调递减,
单调递减,
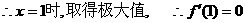 ……………………………2分
……………………………2分
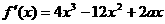
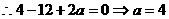 …………………………4分
…………………………4分
(II)点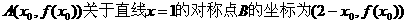 ……6分
……6分
|
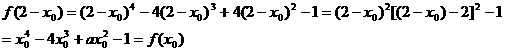
∴A关于直线x=1的对称点B也在函数f(x)的图象上. ………………………9分
(III)函数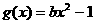 的图象与函数f(x)的图象恰有3个交点,等价于方程
的图象与函数f(x)的图象恰有3个交点,等价于方程
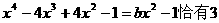 个不等实根. ……………………………10分
个不等实根. ……………………………10分
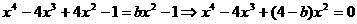 ,
,
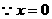 是其中一个根,
是其中一个根,
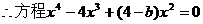 有两个非零不等实根. …………………12分
有两个非零不等实根. …………………12分
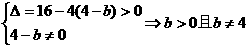 .
…………………………14分
.
…………………………14分
21. (I)由题意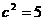 ,
……………2分
,
……………2分
设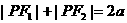 (
(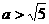 ),由余弦定理, 得
),由余弦定理, 得
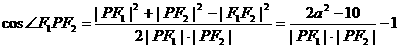 .
.
……………4分
又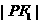 ·
·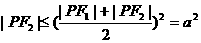 ,
……………6分
,
……………6分
当且仅当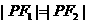 时,
时,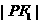 ·
·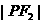 取最大值,
取最大值,
此时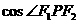 取最小值
取最小值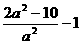 ,令
,令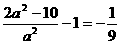 ,
,
解得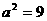 ,
,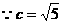 ,∴
,∴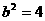 ,故所求
,故所求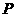 的轨迹方程为
的轨迹方程为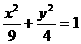 . ……8分
. ……8分
(II)设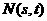 ,
,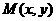 ,则由
,则由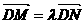 ,可得
,可得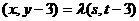 ,
,
故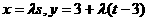 .
…………………10分
.
…………………10分
∵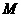 、
、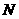 在动点
在动点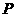 的轨迹上,故
的轨迹上,故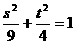 且
且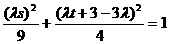 ,
,
消去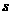 可得
可得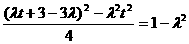 ,解得
,解得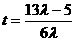 , …………12分
, …………12分
又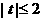 ,∴
,∴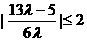 ,解得
,解得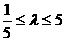 ,
,
故实数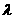 的取值范围是
的取值范围是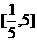 .
………………………14分
.
………………………14分
20.(I)∵在交点处小弹子向左或向右是等可能的,
∴小弹子落入第4层第1个竖直通道的路径只有1条,落入第4层第2个竖直通道的路径有3条,第3个有3条,第4个有1条,∴所求概率P=
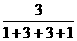 =
=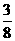 .
.
……………4分
(II)利用杨辉三角的特点可猜想,所求的概率P=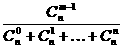 =
=
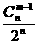 .
.
……………8分
(III) ,即该小弹子落入第
,即该小弹子落入第 层第
层第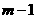 个竖直通道的路径数与该小弹子落入第
个竖直通道的路径数与该小弹子落入第 层第
层第 个竖直通道的路径数之和等于该小弹子落入第
个竖直通道的路径数之和等于该小弹子落入第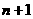 层第
层第 个竖直通道的路径数.
……………12分
个竖直通道的路径数.
……………12分
19. (I)设奖金总数为W万元.则有
W = 64´1 + 32´2 + 16´22 + 8´23 + 4´24 + 2´25 + 1´26 + 27
= 7´26 + 27 = 9´26 (万元). ……………4分
(II) 设门票收入为y元,则
y = 3000[a + ( a + 50 ) + ( a + 100 ) + (a +150) + ( a + 200 ) + ( a +250) + ( a +300 ) ]
= 3000( 7a +1050 ) ……………8分
比赛不亏本,则3000[7a + 1050] ³ 90000´26 .
解得 a ³ 124.3 ……………10分
故要使邀请赛不亏本,第一轮价格至少要定为125元. ……………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com