当问题处在运动状态但结果是定值时，可取其特殊的静止状态进行检验，以避免非智力因素引起的心理性错误。

　 例8. 在正方体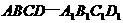中，M、N分别为棱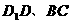的中点，P为棱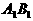上的任意一点，则直线AM与PN所成的角等于________

　　 错解：乱填一个角。

　　 检验：设点P与点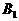重合，则容易证明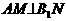，即AM与PN所成角等于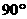。由题意知所求角是个定值，故正确答案为。

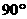　　 当端点处是否成立难以确定时，可直接取其端点进行检验，以避免考虑不周全的错误。

　 例7. 已知关于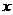的不等式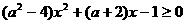的解集是空集，求实数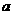的取值范围__________。

　　 错解：由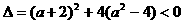，解得。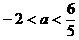

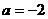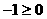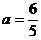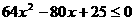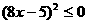　　 检验：若，则原不等式为，解集是空集，满足题意；若，则原不等式为，就是，解得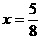，不满足题意。故正确答案为

　　 一种方法解答之后，再用其它方法解之，看它们的结果是否一致，从而可避免单一的方法造成的策略性错误。

　 例6. 若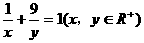，则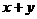的最小值是_________。

　　 错解：，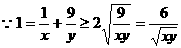

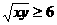
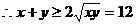
　 检验：上述错解在于两次使用重要不等式，等号不可能同时取到。换一种解法为：

　　 ，

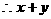　　 的最小值为16。

　　 当问题具有几何背景时，可通过作图进行检验，以避免一些脱离事实而主观意想的错误。

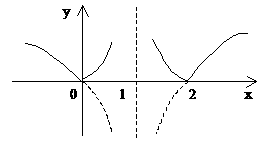
　 例5. 函数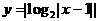的递增区间是___________

　　 错解：()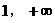

　　 检验：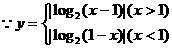

　　 作图可知正确答案为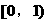与。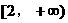

　　 当解题过程中是否等价变形难以把握时，可用估算的方法进行检验，以避免忽视充要条件而产生逻辑性错误。

　 例4. 不等式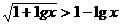的解是 __________

　　 错解：两边平方得，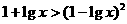

　　 即，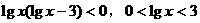

　　 解得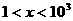

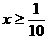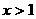　　 检验：先求定义域得。若，则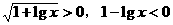，原不等式成立；若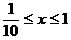时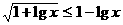，，原不等式不成立。故正确答案为。

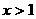　　 若答案是有限的、具体的数据时，可逐一代入进行检验，以避免因扩大自变量的允许值范围而产生增解致错。

　 例3. 方程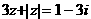的解是__________。

　　 错解：设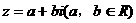，则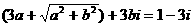，根据复数相等的定义得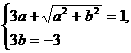

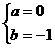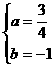
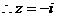　　 解得或

　　 或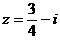

　　 检验：若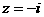，则原方程成立；若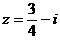，则原方程不成立。故原方程有且只有一解。

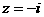　　 若答案是无限的、一般性结论时，可赋予一个或几个特殊值进行检验，以避免知识性错误。

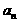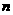　 例2. 已知数列{}的前项和为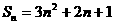，则通项公式=_________。

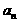　　 错解：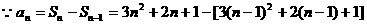

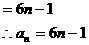
　　 检验　 取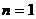时，由条件得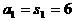，但由结论得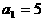。故正确答案为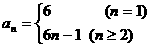

　　 填空题解答之后再回顾，即再审题，这是最起码的一个环节，可以避免审题上带来的某些明显的错误。

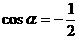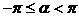　 例1. 满足条件且的角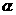的集合 ________。

　　 错解：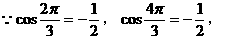

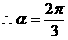　　 或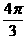

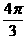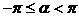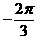　　 检验　 根据题意，答案中的不满足条件，应改为；其次角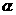的取值要用集合表示。故正确答案为{}。

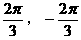22.(本小题满分14分)

定义在(－1，1)上的函数f(x)满足：

①对任意x,y∈(－1,1),都有f(x)+f(y)=f();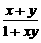

②当x∈(－1,0)时，有f(x)＞0.

(1)判定f(x)在(－1，1)上的奇偶性，并说明理由；

(2)判定f(x)在(－1，0)上的单调性，并给出证明；

(3)求证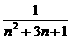：f(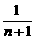)=f()－f(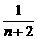)(n∈N).

21.(本小题满分12分)

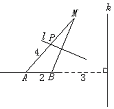如图，A、B是两个定点，且｜AB｜=2，动点M到A点的距离是4，线段MB的垂直平分线l交MA于点P，直线k垂直于直线AB，且B点到直线k的距离为3.

(1)求证：点P到点B的距离与点P到直线k的距离之比为定值；

(2)若P点到A，B两点的距离之积为m，当m取最大值时，求P点的坐标；

(3)若｜PA｜－｜PB｜=1，求cosAPB的值.