
题目列表(包括答案和解析)
设函数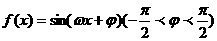 ,给出以下四个论断:
,给出以下四个论断:
(Ⅰ)它的图象关于直线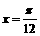 对称;
对称;
(Ⅱ)它的图象关于点(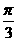 ,0)对称;
,0)对称;
(Ⅲ)它的周期为π;
(Ⅳ)它在区间[- ,0]上是增函数.
,0]上是增函数.
以其中的两个论断为条件,余下的论断为结论,写出你认为正确的两个命题,并对其中一个命题加以证明.
(18)(本小题满分12分)
数列{an}的前n项和为Sn,又数列{bn}满足bn=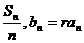 (r为确定的值),求r的值,并证明{an}是等差数列.
(r为确定的值),求r的值,并证明{an}是等差数列.
(19)(本小题满分12分)
如图,
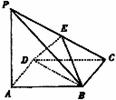
边长为a的菱形ABCD中,A=60°,又PA⊥面ABCD,PA=a,E为CP中点,
(Ⅰ)求证:面BDE⊥面ABCD;
(Ⅱ)求PB与面BDE所成的角大小;
(Ⅲ)求二面角B-DE-C的大小.
(20)(本小题满分12分)
现有流量均为300m3/s的两条河流A、B,汇合于某处后,不断混合,它们的含沙量分别为2kg/m3和0.2kg/m3,假若从汇合处开始,沿岸设有若干个观测点,两股水流在汇经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交流100m3的水量,即从A股流入B股100m3水,经混合后,又从B股流入A股100m3水并混合. (Ⅰ)问从第几个观测点开始,两股河水的含沙量之差小于0.01?kg/m3,(不考虑沙沉淀);
(Ⅱ)随着两股水流的不断混合,它们的含沙量趋向于一个常数,试求出这个常数.
(21)(本小题满分12分)
已知A、B是椭圆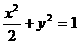 上的两个点,O为坐标原点.
上的两个点,O为坐标原点.
(Ⅰ)若OA⊥OB,|AB|=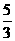 ,求直线OA、OB的方程;
,求直线OA、OB的方程;
(Ⅱ)(文科不做,理科做)若OA⊥OB,求△AOB面积的最小值.
(22)(本小题满分14分)
(理科做)设f(x)=ax2+bx+c(a,b,c∈R)在区间[0,1]上恒有|f(x)|≤1.
(Ⅰ)对所有这样的f(x),求|a|+|b|+|c|最大值;
(Ⅱ)试给出一个这样的f(x),使|a|+|b|+|c|确定达到上述最大值.
(文科做)已知一次函数y=kx+c(c>0),二次函数y=x2的图象交于A、B两点,
(Ⅰ)若k、c为已知常数,求线段AB长度|AB|;
(Ⅱ)若k、c为变动的实数时(c>0),求证:
仅当0<c<1时,有两个k值使|AB|=2.
(13)P是以F1、F2为焦点的双曲线上一点,若PF1⊥PF2,且tgPF1F2=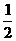 ,
,
则双曲线的离心率等于 .
(14)若已知a>b>c,则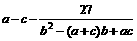 的最小值是
.
的最小值是
.
(15)两腰长均是1的等腰Rt△ABC1和等腰Rt△ABC2所在平面成60°的二面角,则两点C1与C2的距离是 .(写出所有可能的值)
(16)已知(1+xi)4n+2(x∈R,i2=-1)展开式中的实数关于x的多项式,则此多项式系数和为 .
(1)若集合M={x,y,z},集合N={3,0,-3},f是从M到N的映射,则满足f(x)+f(y)+f(z)=0的映射有
?(A)6个 ?(B)7个 ?(C)8个 ?(D)9个
(2)已知集合M={z||z|≤2},N={z|arg(z+1)≤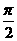 },则M∩N在复平面上对应的图形面积是
},则M∩N在复平面上对应的图形面积是
?(A)2π
(B)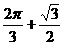 ?(C)
?(C)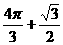 ? (D)
? (D)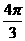
(3)如果函数f(x)是R上的奇函数,在(-1,0)上是增函数,且f(x+2)=-f(x),则下列关系中正确的是
?(A)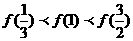 ?
(B)
?
(B) 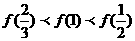
? (C) 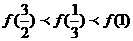 ?(D)
?(D) 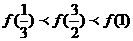
(4)使sinx≤cosx成立的x的一个区间是
?(A)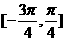 ?
(B)
?
(B)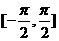
?(C)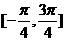 ?(D)[0,π]
?(D)[0,π]
(5)设函数f(x)=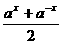 (a为大于1的常数),则使f-1(x)>1的x取值范围是
(a为大于1的常数),则使f-1(x)>1的x取值范围是
?(A)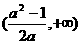 ?
(B)
?
(B)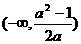
?(C)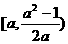 ?(D)(a,+∞)
?(D)(a,+∞)
(6)若无穷等比数列{an}的前n项和为Sn,各项和为S,且S=Sn+2an,则
{an}的公比为
?(A)?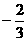 ? (B)
? (B)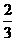 ?(C)
?(C)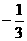 ? (D)
? (D)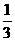
(7)一棱锥被平行于底面的平面截成一个小棱锥和一个棱台,若小棱锥及棱台的体积分别是y和x,则y关于x的函数图象大致形状为

(8)在正三棱锥P-ABC中,E、F分别为PA、AB的中点,∠CEF=90°,若AB=a,则该三棱锥的体积为
(A)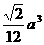 ? (B)
? (B) 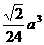 ? (C)
? (C) 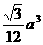 ? (D)
? (D) 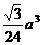 ?
?
(9)4个茶杯和5包茶叶的价格之和小于22元,而6个茶杯与3包茶叶的价格之和大于24元,则2个茶杯和3包茶叶的价格比较
(A)2个茶杯贵 ?(B)3包茶叶贵 ?(C)?相同 ?(D)?无法确定
(10)已知圆x2+y2=5x内,过点(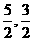 )有n条弦的长成等差数列,最短弦长为数列的首项a1,最长弦长为an,若公差d∈(
)有n条弦的长成等差数列,最短弦长为数列的首项a1,最长弦长为an,若公差d∈(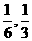 ),那么n的值构成的集合为
),那么n的值构成的集合为
(A){6,7,8,9} ?(B){3,4,5,6}
(C){3,4,5} ?(D){4,5,6}
(11)已知集合A={1,2,4,8,…,2n}(n≥3,n∈N),集合A中含有三个元素的所有子集依次为B1,B2,…,Bm.若Bi中所有元素之和为ai(i=1,2,…,m)则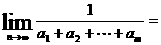
?(A)2 ?(B)1 ?(C)0 ?(D)不存在
(12)对一切实数x,不等式x4+ax2+1≥0恒成立,则实数a的取值范围是
?(A)(-∞,-2) ?(B)[-2,+∞]
? (C)[0,2] ?(D)[0,+∞]
第Ⅱ卷(非选择题 共90分)
20.(本小题满分12分)
(理科学生作)已知二次函数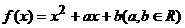 的定义域为[-1,1],
的定义域为[-1,1],
且|f(x)|的最大值为M。
(Ⅰ)试证明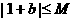 ;
;
(Ⅱ)试证明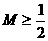 ;
;
(Ⅲ)当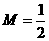 时,试求出f(x)的解析式。
时,试求出f(x)的解析式。
(文科学生作)设二次函数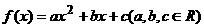
若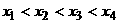 且
且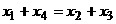
(Ⅰ)试证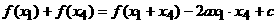
(Ⅱ)试比较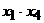 与
与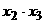 之间的大小关系。
之间的大小关系。
(Ⅲ)试比较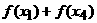 与
与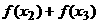 之间的大小关系。
之间的大小关系。
19.(本小题满分16分)
已知数列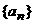 中,
中,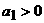 ,且
,且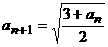 。
。
(Ⅰ)试求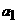 的值,使得数列
的值,使得数列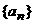 是一个常数数列;
是一个常数数列;
(Ⅱ)试求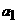 的取值范围,使得
的取值范围,使得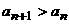 对任何自然数n都成立;
对任何自然数n都成立;
(Ⅲ)若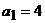 ,设
,设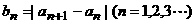 ,并以
,并以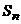 表示数列
表示数列 的前n项的和,试证明:
的前n项的和,试证明: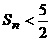 。
。
18.(本小题满分12分)
经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量f(n)(万件)近似地满足下列关系: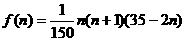 (n=1,2,3,…,12)
(n=1,2,3,…,12)
(Ⅰ)写出明年第n个月这种商品需求量g(n)(万件)与月份n的函数关系式,并求出哪几个月的需求量超过1.4万件;
(Ⅱ)若计划每月该商品的市场投放量都是p万件,并且要保证每月都满足市场需求,则p至少为多少万件?
17.(本小题满分14分)
已知一次函数y=f(x)满足f(0)=1,又点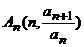 (n=1,2,3,…)在这个一次函数y=f(x)的图像上,若
(n=1,2,3,…)在这个一次函数y=f(x)的图像上,若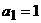 ,且当
,且当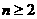 时,恒有
时,恒有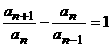
(Ⅰ)求f(x)的解析式;
(Ⅱ)分别写出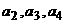 的值,并求出数列
的值,并求出数列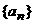 的通项公式。请予以证明。
的通项公式。请予以证明。
16.(本小题满分12分)
已知复数z满足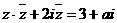 其中a是实数
其中a是实数
(Ⅰ)求复数z(写成关于a的表达式)
(Ⅱ)当实数a为何值时,满足条件的复数z存在?
15.(本小题满分14分)
(理科学生作)解关于x的不等式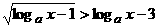 其中0<a<1
其中0<a<1
(文科学生作)解不等式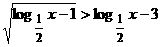
14.从3男7女共10个人中选出5人,
若其中甲、乙两人必选在内,共有___________种不同的选法;(用数字作答)
若至少有一名男生被选在内,共有___________种不同的选法。(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com