
题目列表(包括答案和解析)
(17)(本小题满分12分)
解关于x的不等式: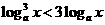 (
( 且
且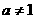 ).
).
(18)(本小题满分12分)
已知正项数列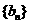 的前n项和
的前n项和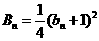 ,求
,求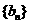 的通项公式.
的通项公式.
(19)(本小题满分12分)
已知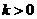 ,直线l1:y=kx,l2:y=-kx.
,直线l1:y=kx,l2:y=-kx.
(Ⅰ)证明:到l1、l2的距离的平方和为定值a(a>0)的点的轨迹是圆或椭圆
(Ⅱ)求到l1、l2的距离之和为定值c(c>0)的点的轨迹.
(20)(本小题满分12分)
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=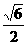 a,
a,
(Ⅰ)求异面直线AC与BC1所成角的余弦值;
(Ⅱ)求证:A1B⊥面AB1C.
(21)(本小题满分12分)
已知盒中有10个灯泡,其中8个正品,2个次品.现需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次品,求ξ的分布列及Eξ.
(22)(本小题满分14分)
已知抛物线C: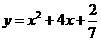 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(Ⅰ)若C在点M的法线的斜率为-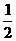 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(Ⅱ)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
(13)抛物线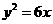 的准线方程为
.
的准线方程为
.
(14)在5名学生(3名男生,2名女生)中安排2名学生值日,其中至少有1名女生的概率是 .
(15)函数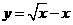 (
(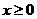 )的最大值为
.
)的最大值为
.
(16)若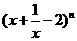 的展开式中常数项为-20,则自然数n= .
的展开式中常数项为-20,则自然数n= .
(1)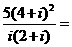
(A)5(1-38i) (B)5(1+38i) (C)1+38i (D)1-38i
(2)不等式|2x2-1|≤的解集为
(A)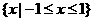 (B)
(B)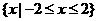
(C)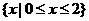 (D)
(D)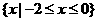
(3)已知F1、F2为椭圆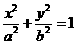 (
(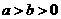 )的焦点;M为椭圆上一点,MF1垂直于x轴,且∠F1MF2=600,则椭圆的离心率为
)的焦点;M为椭圆上一点,MF1垂直于x轴,且∠F1MF2=600,则椭圆的离心率为
(A)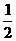 (B)
(B)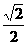 (C)
(C)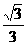 (D)
(D)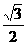
(4)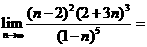
(A)0 (B)32 (C)-27 (D)27
(5)等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所处的二面角为300,则四棱锥A-MNCB的体积为
(A)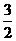 (B)
(B)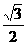 (C)
(C)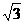 (D)3
(D)3
(6)已知数列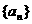 满足
满足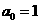 ,
,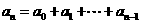 (
(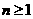 ),则当
),则当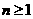 时,
时,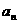 =
=
(A)2n (B)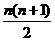 (C)2n-1 (D)2n-1
(C)2n-1 (D)2n-1
(7)若二面角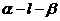 为1200,直线
为1200,直线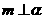 ,则
,则 所在平面内的直线与m所成角的取值范围是
所在平面内的直线与m所成角的取值范围是
(A)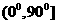 (B)[300,600] (C)[600,900] (D)[300,900]
(B)[300,600] (C)[600,900] (D)[300,900]
(8)若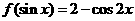 ,则
,则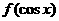 =
=
(A)2-sin2x (B)2+sin2x (C)2-cos2x (D)2+cos2x
(9)直角坐标xOy平面上,平行直线x=n(n=0,1,2,……,5)与平行直线y=n(n=0,1,2,……,5)组成的图形中,矩形共有
(A)25个 (B)36个 (C)100个 (D)225个
(10)已知直线l:x―y―1=0,l1:2x―y―2=0.若直线l2与l1关于l对称,则l2的方程是
(A)x―2y+1=0 (B)x―2y―1=0 (C)x+y―1=0 (D)x+2y―1=0
(11)已知向量集合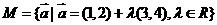 ,
,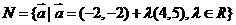 ,则
,则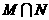 =
=
(A){(1,1)} (B){(1,1),(-2,-2)}
(C){(-2,-2)} (D)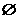
(12)函数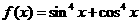 的最小正周期为
的最小正周期为
(A)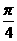 (B)
(B)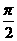 (C)
(C)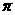 (D)2
(D)2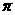
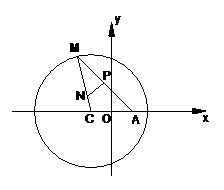
16、如图所示,已知圆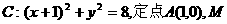 为圆上一动点,点P在A上,
为圆上一动点,点P在A上,
点N在CM上,且满足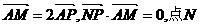 的轨迹为曲线E.(I)求曲线E的方程;(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
的轨迹为曲线E.(I)求曲线E的方程;(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
 且满足
且满足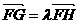 ,求
,求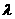 的取值范围.
的取值范围.
15、已知A、B、C是直线m上的三点,且|AB|=|BC|=6,⊙O′切直线m于点A,又过B、C作⊙O′异于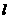 的两切线,切点分别为D、E,设两切线交于点P,(1)求点P的轨迹方程
的两切线,切点分别为D、E,设两切线交于点P,(1)求点P的轨迹方程
(2)经过点C的直线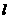 与点P的轨迹交于M、N两点,且点C分
与点P的轨迹交于M、N两点,且点C分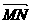 所成比等于2∶3,
所成比等于2∶3,
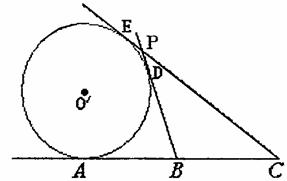 求直线
求直线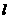 的方程.
的方程.
14、已知函数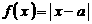 ,
,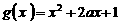 (
(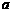 为正常数),且函数
为正常数),且函数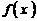 与
与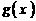 的图象在
的图象在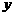 轴上的截距相等。(1)求
轴上的截距相等。(1)求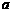 的值; (2)求函数
的值; (2)求函数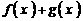 的单调递增区间;
的单调递增区间;
(3)若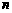 为正整数,证明:
为正整数,证明: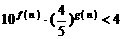 .
.
13、记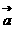 =(
=(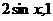 ),
),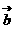 =(
=(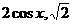 ),且0
),且0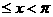 (1)若向量
(1)若向量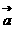 与
与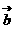 的夹角为锐角,求实数x的取值范围。(2)若
的夹角为锐角,求实数x的取值范围。(2)若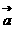 //
//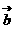 ,且
,且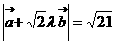 ,求实数
,求实数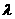 。
。
12、在某次数学测验中,学号为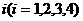 的四位同学的考试成绩
的四位同学的考试成绩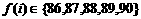
且满足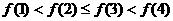 ,则四位同学的考试成绩的所有可能情况有 种(用数字作答).
,则四位同学的考试成绩的所有可能情况有 种(用数字作答).
11、给定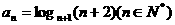 ,定义使
,定义使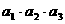 ……
……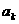 为整数的数
为整数的数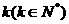 叫做企盼数,则区间(1,2004)内的所有企盼数的和M=
。
叫做企盼数,则区间(1,2004)内的所有企盼数的和M=
。
10、已知铜的单晶体的外形是简单几何体,单晶体有三角形和八边形两种晶面,如果铜的单晶体有24个顶点,每个顶点处有3条棱,那么单晶铜的三角形晶面和八边形晶面的数目分别为 和 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com