
题目列表(包括答案和解析)
4.集合M={(x,y)|y=-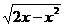 },N={(x,y)|y=kx-3k+1},若M∩N≠Ф,则k的取值范围是
( )
},N={(x,y)|y=kx-3k+1},若M∩N≠Ф,则k的取值范围是
( )
A、[0,1] B、[0,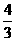 ] C、[
] C、[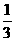 ,1] D、[
,1] D、[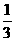 ,
,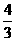 ]
]
3.已知f(x)=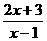 ,函数y=g(x)的图象与y=f-1(x+1)的图象关于直线y=x对称,则g(3)等于
( )
,函数y=g(x)的图象与y=f-1(x+1)的图象关于直线y=x对称,则g(3)等于
( )
A、3
B、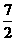 C、
C、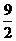 D、
D、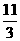
2.设f(x)的定义域为R,a、b是两个常数且b>a,如果对于任何x∈R均有f(x+a)=f(x+b),那么对于任何x∈R,n∈Z,均有f(x)= ( )
A、f[x+n(a+b)] B、f[x-n(a+b)]
C、f[x-n(a-b)] D、f(x)-n(a-b)
1.向量 =(cosα,sinα,
=(cosα,sinα,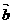 =(cosβ,sinβ),其中α=β+
=(cosβ,sinβ),其中α=β+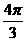 ,则
,则 与
与 +
+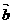 的夹角为 ( )
的夹角为 ( )
A、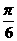 B、
B、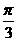 C、
C、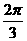 D、
D、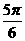
22.(本小题满分14分)
已知函数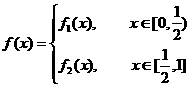
其中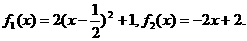
(1)画出y=f(x)的图象;
(2)求y= f(x)的反函数;
(3)设y=g(x)与y= f(x)的图象关于x=-1对称,求y= g(x)的解析式,并写出y= g(x)的单调区间.
21.(本小题满分12分)
设x , y ∈R, 、
、 为直角坐标系内x、y轴正方向上的单位向量,若
为直角坐标系内x、y轴正方向上的单位向量,若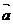 =x
=x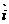 +(y+2)
+(y+2)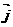 ,
,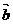 =x
=x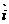 +(y-2)
+(y-2) 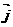 且
且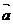 2+
2+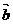 2=16.
2=16.
(1)求点M(x, y )的轨迹C 的方程;
(2)过定点(0,3)作直线l与曲线C交于A、B两点,设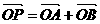 ,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
,是否存在直线l使四边形OAPB为正方形?若存在,求出l的方程,若不存在说明理由.
20.(本小题满分12分)
已知圆C:x2+y2=25及直线l:mx-y-2m+1=0(m∈R).
(1)证明:无论m取什么实数,直线l与圆C恒相交;
(2)求直线l被圆C截得弦长的最小值及此时 的直线方程.
9.如图,已知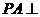 面
面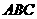 ,
,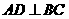 于D,
于D,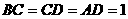 .
.
(I)令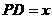 ,
,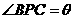 ,试把
,试把 表示为
表示为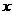 的函数,并求其最大值;
的函数,并求其最大值;
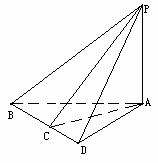 (II)在直线PA上是否存在一点Q,使得
(II)在直线PA上是否存在一点Q,使得
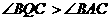 ?
?
18.(本小题满分12分)
已知等差数列{an}中,a4+a7+a10=17,a4+a5+a6+…+a14=77.
(1)求{ an}的公差d和a1;
(2)若Sk=64,求k的值.
17. (本小题满分10分)
已知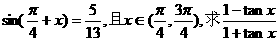
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com