
题目列表(包括答案和解析)
5.设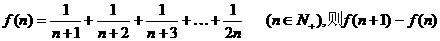 等于 ( )
等于 ( )
A.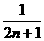 B.
B.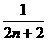 C.
C.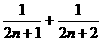 D.
D.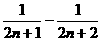
4.在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2a10-a12的
值为 ( )
A.20 B.22 C.24 D.28
3.下面的四个命题
①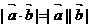 ②
②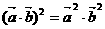
③若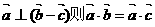 ④若
④若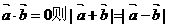
其中真命题是 ( )
A.①② B.③④ C.①③ D.②④
2.已知集合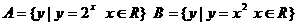 则 ( )
则 ( )
A. B.
B.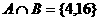
C.A=B D.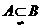
1.满足f(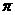 +x)=-f(x),f(-x)=f(x)的函数f(x)可能是
( )
+x)=-f(x),f(-x)=f(x)的函数f(x)可能是
( )
A.cos2x B.sinx C.sin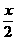 D.cosx
D.cosx
22.(本小题满分14分)
已知函数f(x)=x4-4x3+ax2-1在区间[0,1)上单调递增,在区间[1,2)上单调递减.
(Ⅰ)求a的值;
(Ⅱ)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(Ⅲ)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点.若存在,请求出实数b的值;若不存在,试说明理由.
21.(本小题满分12分)
给定双曲线x2-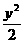 =1,
=1,
(Ⅰ)过点A(2,1)的直线l与所给双曲线交于P1 、P2,求线段P1P2的中点P的轨迹方程;
(Ⅱ)过点B(1,1)能否作出直线l′,使l′与所给双曲线交于两点Q1 、Q2,且B是线段Q1Q2的中点?说明理由.
20.(注意:在以下甲、乙两题中任选一题作答.如果两题都作答,只以甲题记分,本小题满分12分)
(甲)如图,已知正四棱锥S-ABCD,底面的中心O为坐标原点,建立空间直角坐标系O-xyz,其中Ox//BC、Oy//AB,四棱锥的底面的边长为4,高为6,点M是高SO的中点,G是侧面△SBC的重心.求
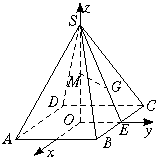
(Ⅰ)MG两点间的距离;
(Ⅱ)异面直线MG与BS所成的角.
(乙)如图,三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P-AC-B为120°,PC = 2,AB=2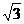 .
.
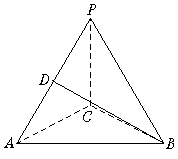
(Ⅰ)求证:AC⊥BD;
(Ⅱ)求BD与底面ABC所成角的正弦值.
19.(本小题满分12分)
已知数列1,3,6…的各项是由一个等比数列和一个等差数列的对应项相加而得到,其中等差数列的首项为0.
(Ⅰ)求这个数列的前n项和Sn;
(Ⅱ)设Tn=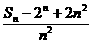 ,问是否存在正整数M,使得对一切正整数n,Tn≤M都成立.如存在,求出M的最小值;如不存在,说明理由.
,问是否存在正整数M,使得对一切正整数n,Tn≤M都成立.如存在,求出M的最小值;如不存在,说明理由.
(Ⅲ)求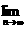 Tn的值.
Tn的值.
18.(本小题满分12分)
在袋里装30个小球,其中彩球有:n个红色、5个蓝色、10个黄色,其余为白色.
求:(Ⅰ)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
(Ⅱ)如果从袋里取出3个都是相同颜色彩球(无白色)的概率是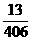 ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?
(Ⅲ)根据(Ⅱ)的结论,计算从袋中任取3个小球至少有一个是红球的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com