8．“a>b，b>c”是“a>c”的( )

7．“x=1”是“x²-2x+1=0”的( )

6．“|x|>1”是“x>1”的( )

5．“a>b”是“a+c>b+c”的( )

4．“a>b”是“ac²>bc²”的( )

3．“a=b”是“ac=bc”的( )

2．“a>b”是“a²>b²”的( )

1．“x>-1”是“x>1”的( )

7．充要条件

　　 (1)对充要条件的理解

　　 对于命题“若p则q”，即p是条件，q为结论．

　　 ①如果由p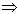q，则p是q的充分条件

　　 ②如果由q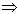p，则p是q的必要条件

　　 ③如果pq，则p是q的充要条件，q也是p的充要条件

　　 如x>0是x²>0的充分条件；x²>0是x>0的必要条件；x≠0是x²>0的充要条件，x²>0也是x≠0的充要条件，

充要条件是相互的．

　　 (2)充要条件的判断．

　　 充要条件的判断主要以选择题形式出现，

　　 如在△ABC中，A>B是a>b的 ( )

　　 A．充分条件 B．必要条件

　　 C．充要条件 D．非充分非必要条件　　　　 本题选(C)

　　 ①直接用充要条件定义判断

　　 ②借助四种命题之间的关系间接判断，如所给命题的条件不易判断，我们可以转化为判断它的逆否命题

的条件，因为原命题与其逆否命题是等价的，即同真或同假．反证法就是一种间接法．

例题分析：

第一阶梯

　 例1．分别指出下列复合命题的形式及构成它的简单命题：

　　 ①1既不是质数，也不是合数；

　　 ②0不是奇数；

　　 ③斜三角形的内角是锐角或是钝角．

　　 解：①这个命题是p且q的形式，其中p：1不是质数；q：1不是合数

　　　　 ②这个命题是非p的形式，其中p：0是奇数

　　　　 ③这个命题是p或q的形式，其中p：斜三角的内角是锐角，q：斜三角形的内角是钝角．

　 反思回顾：在①中，p和q两个命题还是非p形式的．

　 例2． 选择题

6．反证法

　　 ①反证法的理论根据是：原命题为真，则它的逆否命题也为真．在直接证明原命题有困难时，就可转化

为证明它的逆否命题成立．

　　 ②用反证法证明命题的一般步骤是

　　 第一步：假设命题的结论不成立，即假设结论的反面成立；

　　 第二步：从这个假设出发，经过推理论证，得出矛盾：

　　 第三步：由矛盾判定假设不正确，从而肯定命题的结论正确．

　　 ③一般地来说，在什么条件下(或问题中)想到用反证法来证明，下面提供几种情形作为参考．

　　 第一，问题共计有n种情况，现要证明其中一种情况成立时，可想到用反证法证明把其他的n-1种情况都

排除，从而确定这种情况成立．

　　 如，要证明两条直线相交，可用反证法证明这两条直线平行不成立，因为在同一平面内，两条直线的位

置关系是平行或相交，平行不成立，那么间接证明了两条直线相交；

　　 第二，命题用否定形式叙述的，如证明2不是方程2x+1=0的根，可用反证法证明，假设2是方程2x+1=0的

根，则2×2+1应等于0，而2×2+1=5，产生矛盾，从而确定2不是方程2x+1=0的根成立；

　　 第三，命题用“至少”的字样叙述时，可用反证法证明，如证明a≠b，b≠c至少有一个成立，那我们可

用反证法证明如下：假设a≠b，b≠c都不成立，即a=b且b=c，从这一条件出发推得矛盾，a=b，且b=c不成

立，因此，a≠b，b≠c至少有一个成立；

　　 第四，当命题成立非常明显，要直接证明，所用的理论不少，但不容易说明白，而它的逆否命题易证，

如上面的例子，证明两条直线相交的依据几乎没有，而证明平行线有很多性质，易于推理，因此，用反证法

把证明两条直线相交问题转化到平行的性质．