
题目列表(包括答案和解析)
24.本小题主要考查概率统计的基础知识,运用数学知识解决问题的能力.满分12分.
解:(Ⅰ)依题意,甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
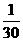 |
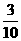 |
 |
 |
甲答对试题数ξ的数学期望
Eξ=0×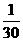 +1×
+1×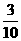 +2×
+2× +3×
+3× =
= .
.
(Ⅱ)设甲、乙两人考试合格的事件分别为A、B,则
P(A)= =
=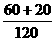 =
= ,
,
P(B)= =
= =
= .
.
因为事件A、B相互独立,
方法一:
∴甲、乙两人考试均不合格的概率为
P( )=P(
)=P( )P(
)P( )=1-
)=1- )(1-
)(1- )=
)= .
.
∴甲、乙两人至少有一人考试合格的概率为
P=1-P( )=1-
)=1- =
= .
.
答:甲、乙两人至少有一人考试合格的概率为 .
.
方法二:
∴甲、乙两人至少有一个考试合格的概率为
P=P(A· )+P(
)+P( ·B)+P(A·B)=P(A)P(
·B)+P(A·B)=P(A)P( )+P(
)+P( )P(B)+P(A)P(B)
)P(B)+P(A)P(B)
= ×
× +
+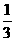 ×
× +
+ ×
× =
= .
.
答:甲、乙两人至少有一人考试合格的概率为 .
.
24.(2004. 福建理)(本小题满分12分)
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲答对试题数ξ的概率分布及数学期望;
(Ⅱ)求甲、乙两人至少有一人考试合格的概率.
23.解:(Ⅰ)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
|

由①、③得 代入②得 27[P(C)]2-51P(C)+22=0.
代入②得 27[P(C)]2-51P(C)+22=0.
解得
 (舍去).
(舍去).
将
 分别代入
③、② 可得
分别代入
③、② 可得 
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是
(Ⅱ)记D为从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的事件,
则

故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为
23.(2004.湖南理)(本小题满分12分)
甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为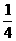 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率
22.(2004.湖北理)将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 240
种.(以数字作答)
21、(2004.上海理)若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是  . (结果用分数表示)
. (结果用分数表示)
20.(2004. 福建理).某射手射击1次,击中目标的概率是0.9.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14.
其中正确结论的序号是 1,3 (写出所有正
确结论的序号).
19. (2004. 重庆理)若在 的展开式中
的展开式中 的系数为
的系数为 ,则
,则 .-2
.-2
18.(04. 上海春季高考)如图,在由二项式系数所构成的杨辉三角形中,第
 ___34 __行中从左至右第14与第15个数的比为
___34 __行中从左至右第14与第15个数的比为 .
.
17.(04. 上海春季高考)一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇。若任意排列交流次序,则最先和最后交流的论文都为试点学校的概率是__________ (结果用分数表示).
(结果用分数表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com