
题目列表(包括答案和解析)
19. .( 本小题满分12分)
经过抛物线y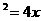 的焦点F的直线L与该抛物线交于A,B两点.
的焦点F的直线L与该抛物线交于A,B两点.
(1) 若线段AB的斜率为k,试求中点M的轨迹方程;
(2) 若直线的斜率k>2,且点M到直线3 x+4y+m=0的距离为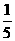 ,试确定m的取值范围。
,试确定m的取值范围。
18.
 .( 本小题满分12分)
.( 本小题满分12分)
如图,正三角形ABC与直角三角形BCD成直二面角,
且∠BCD=90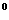 ,∠CBD=30
,∠CBD=30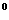 .
.

 (1) 求证:AB⊥CD;
B
C
(1) 求证:AB⊥CD;
B
C
(2)求二面角D-AB-C的正切值。 D
(3)[理]求异面直线AC和BD所成的角。
17.( 本小题满分12分)
已知复数z=sinB+(1-cosB)i ,argz=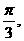 A, B, C是⊿ABC的内角。
A, B, C是⊿ABC的内角。
(1)求B; (2)求sinA+sinC的取值范围。 A
15.某校有学生宿舍若干间,现安排高三女生居住,若每间住5人,余60人. 若每间住10人,则有一间宿舍不空也不满,则高三女生有 人,宿舍有 间.
16已知双曲线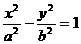 的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
的左支上存在一点P到左焦点的距离是点P到右焦点距离和到左准线距离的比例中项,则双曲线的离心率e的取值范围是
.
14.一个圆柱形容器的内半径为5cm,两个直径为5的玻璃小球被浸没于容器的水中,当取出这两个小球后, 容器的水面下降了x cm, 则x= .
13.[文] 已知函数f(x)=2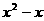
 ,则使得数列
,则使得数列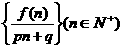 成等差数列的非零常数p与q所满足的关系式为
.
成等差数列的非零常数p与q所满足的关系式为
.

 [理]在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1=
[理]在下面等号右侧两个分数的分母方块处,各填上一个自然数,并且使这两个自然数的和最小:1= .
.
12.对某种产品的6件不同正品和4件不同次品一一进行测试,到区分出所有次品为止。若所有次品恰好在第五次测试被全部发现,则这样的测试方法有( )
A.24种 B.96种 C.576种 D.720种
第Ⅱ卷 (非选择题,共90分)
11. 若L是过椭圆一个焦点且与长轴不重合的一条直线,则此椭圆与L垂直且被L平分的弦( )
A.有且只有一条 B. 有且只有2条
C.有3条 D. 不存在
10.[理] 已知A,B,C,D是同一球面上的四点,且连接每两点的线段长都等于2,则球心到平面BCD的距离为( )
A.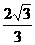 B.
B.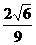 C.
C.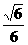 D.
D.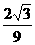
[文] 有一棱长为a的正方体框架,其内放置一气球,是其充气且尽可能地膨胀(仍保持为球的形状),则气球表面积的最大值为( )
A.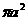 B.2
B.2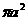 C.3
C.3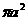 D.4
D.4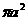
9.在圆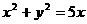 内,过点
内,过点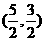 有n条弦的长度成等差数列,最短弦长为数列的首项
有n条弦的长度成等差数列,最短弦长为数列的首项 ,最长弦长为
,最长弦长为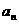 ,若公差
,若公差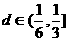 ,则n的取值集合为 ( )
,则n的取值集合为 ( )
A.{4,5,6} B.{6,7,8,9} C.{3,4,5} D.{3,4,5,6}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com