
题目列表(包括答案和解析)
19.(本题满分12分)
某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
(1)写出服药后y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药时间为上午7:00,问一天中怎样安排服药的时间(共4次)效果最佳?
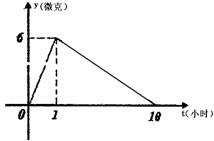
解:(1)依题得,y=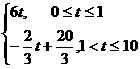
(2)设第二次服药时在第一次服药后t1小时,则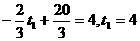 因而第二次服药应在11:00;
因而第二次服药应在11:00;
设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药量的和,即有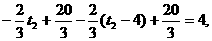 解得t2=9小时,故第三次服药应在16:00;
解得t2=9小时,故第三次服药应在16:00;
设第四次服药在第一次后t3小时(t3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和,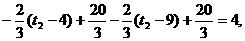 解得
解得
t3=13.5小时,故第四次服药应在20:30.
18.(本题满分12分)
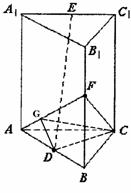
如图,正三棱柱AC1中,AB=2,D是AB的中点,E是A1C1的中点,F是B1B中点,异面直线CF与DE所成的角为90°.
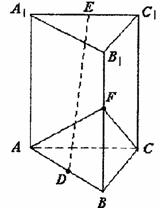 (1)求此三棱柱的高;
(1)求此三棱柱的高;
(2)求二面角C-AF-B的大小.
解:(1)取BC、C1C的中点分别为H、N,连结HC1,
连结FN,交HC1于点K,则点K为HC1的中点,因
FN//HC,则△HMC∽△FMK,因H为BC中点
BC=AB=2,则KN=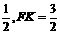 ,∴
,∴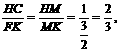
则HM=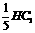 ,在Rt△HCC1,HC2=HM·HC1,
,在Rt△HCC1,HC2=HM·HC1,
解得HC1=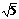 ,C1C=2.
,C1C=2.
另解:取AC中点O,以OB为x轴,OC为y轴,按右手系建立空间坐标系,设棱柱高为h,则C(0,1,0),F(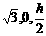 ),D(
),D( ),E(0,0,h),
),E(0,0,h),
 ∴
∴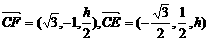 ,由CF⊥DE,得
,由CF⊥DE,得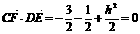 ,解得h=2.
,解得h=2.
(2)连CD,易得CD⊥面AA1B1B,作DG⊥AF,连CG,
由三垂线定理得CG⊥AF,所以∠CGD是二面角C-AF-B
的平面角,又在Rt△AFB中,AD=1,BF=1,AF=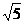 ,
,
从而DG=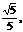 ∴tan∠CGD=
∴tan∠CGD=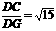 ,
,
故二面角C-AF-B大小为arctan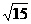 .
.
17.(本小题满分12分)
已知A、B、C的坐标分别为A(3,0),B(0,3),C(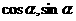 ),
),
(I)若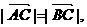 求角
求角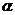 的值;
的值;
(II)若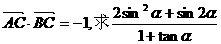 的值.
的值.
解:(1)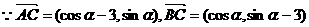
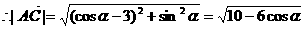 ,
,
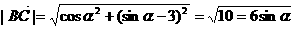 .
.
由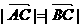 得
得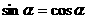 .
又
.
又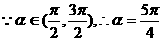 .(2)由
.(2)由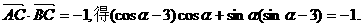
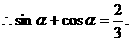 ①又
①又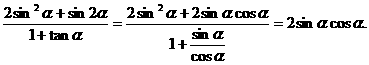 由①式两分平方得
由①式两分平方得
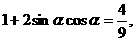
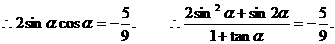
16.若函数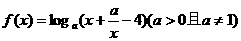 的值域是R,则实数a的取值范围
的值域是R,则实数a的取值范围
是(0,1)∪(1,4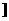
15.(理)定义运算: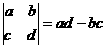 ,若复数
,若复数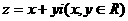 满足
满足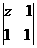 的模等于x,则复数z对应的Z(x,y)的轨迹方程为:
的模等于x,则复数z对应的Z(x,y)的轨迹方程为: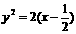 ;
;
14.设非零复数x,y满足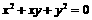 ,则代数式
,则代数式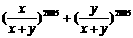 的值是1.
的值是1.
13.当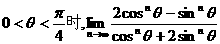 =2
=2
12.已知定义在R上的函数y=f(x)满足下列三个条件:①对任意的x∈R都有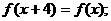 ②对于任意的
②对于任意的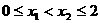 ,都有
,都有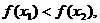 ③
③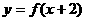 的图象关于y轴对称,则下列结论中,正确的是 (B)
的图象关于y轴对称,则下列结论中,正确的是 (B)
A.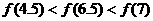 B.
B.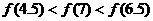
C.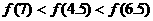 D.
D.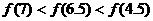
11.一机器狗每秒钟前进或后退一步,程度设计师让机器狗以前进3步,然后再后退2步的规律移动. 如果将此机器狗放在数轴的原点,面向正的方向,以1步的距离为1单位长,令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0,那么下列结论中错误的是 (D)
A.P(3)=3 B.P(5)=1
C.P(101)=21 D.P(103)<P(104)
10. 将3种农作物都种植在如图的4块试验田里,每块种值一种
将3种农作物都种植在如图的4块试验田里,每块种值一种
农作物,要求相邻的试验田不能种植同一种作物,则不同的
种植方法共有 (C)
A.6种 B.12种 C.18种 D.24种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com