
题目列表(包括答案和解析)
8. 已知函数y=f(x)是R上的偶函数,且在[0,+∞]上是减函数,若f(m)≤f (3),则实数m的取值范围是( )
A.m≥3 B.m≤-3 或m≥3 C. .m≤-3 D. m≥3
7.[理] 若直线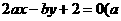 、b〉0)始终平分圆
、b〉0)始终平分圆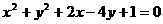 的周长,则
的周长,则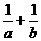 的最小值是( )
的最小值是( )
A. 4
B. 2 C.
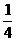 D.
D.
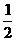
[文] 若直线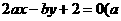 、b〉0)过圆
、b〉0)过圆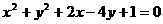 的圆心,则ab的最大值为( )
的圆心,则ab的最大值为( )
A.. 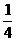 B.
B.
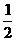 C.
1
D.2
C.
1
D.2
6. 已知函数y=sinx-cosx,给出以下四个命题,其中正确的命题是( )
A. 若x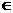 [
[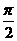 ,
,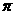 ],则y
],则y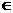 [0,
[0,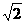 ]
]
B. 在区间[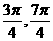 ]上是增函数
]上是增函数
C. 直线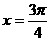 是函数图像的一条对称轴
是函数图像的一条对称轴
D. 函数的图像可由函数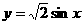 的图像向左平移
的图像向左平移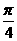 个单位得到
个单位得到
5.
[理] 极坐标系中,点(1,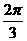 )到圆
)到圆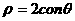 上动点的距离的最大值为( )
上动点的距离的最大值为( )
A. B.
B. C.2
D.1
C.2
D.1
[文] 奇函数f(x)在[3,7]上是增函数,在[3,6]上的最大值为8,最小值为-1,则2f(-b)+f(-3)=( )
A.5 B.-5 C.-13 D.-15
4.



 如图示,向放在水槽底部的烧杯注水(流量一定),
如图示,向放在水槽底部的烧杯注水(流量一定),
注满烧杯后,继续注水,直至注满水槽,水槽中水面
上升高度h与注水时间t之间的函数关系大致是下列










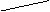
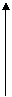







 图像中的( )
图像中的( )
h h
0 t 0 t
A B
h h
0 t 0 t
C D
3.已知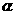 与L分别是一个平面和一条直线,则
与L分别是一个平面和一条直线,则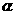 内至少有一条直线与直线L( )
内至少有一条直线与直线L( )
A.平行 B.相交 C.异面 D.垂直
2. 在△ABC中,“sin2A> ”
” 是“A>15
是“A>15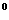 ”的( )
”的( )
A.充分不必要条件 B。必要不充分条件
C.充要条件 D。既不充分也不必要条件
1. 已知集合P={ 0, m},Q={x│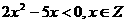 },若P∩Q≠
},若P∩Q≠ ,则m等于( )
,则m等于( )
A.1
B.2
C.1或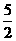 D. 1或2
D. 1或2
19、(本小题满分14分)
本题考查函数与绝对值不等式的综合应用,考查综合分析问题和解决问题的能力,充分考查综合应用知识的能力。
证明:(1)∵f(0)=f(1) ∴b=1+a+b ∴a=-1 ∴f(x)=x3-x+b
设(x0,y0)是y=f(x)的图象上的任意一点,则y0=f(x0)=x03-x0+b
∴-y0=-x03+x0-b=(-x03)-(-x0)-b
∴2b-y0=(-x03)-(-x0)+b
故点(- x0,2b-y0)也在y=f(x)的图象上
又点(x0,y0)与点(-x0,2b-y0)关于点(0,b)对称,进而有点(x0,y0)的任意性,得函数f(x)的图象关于点(0,b)成中心对称图形
所以函数f(x)的图象是中心对称图形,且对称中心为点(0,b)(5分)
解法二:(1)∵f(0)=f(1) ∴b=1+a+b ∴a=-1 ∴f(x)=x3-x+b
易知y=x3-x是奇函数,它的图象关于原点对称;而函数f(x)=x3-x+b的图象可由y=x3-x的图象向上平移b个单位得到,故函数f(x)=x3-x+b的图象关于(0,b)对称
所以函数f(x)的图象是中心对称图形,且对称中心为点(0,b)(5分)
(2)∵y1=x13-x1+b,y2=x23-x2+b
∴y1-y2=(x13-x1)-(x23-x2)=(x1-x2)(x12+x22+x1x2-1)
∵x1≠x2
∴k=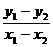 =x12+x22+x1x2-1
=x12+x22+x1x2-1
∵x1,x2∈[-1,1],x1≠x2
∴3>x12+x1x2+x22>0,
-1<x12+x1x2+x22-1<2
∴|x12+x1x2+x22-1|<2
即|k|<2(10分)
(3)∵∴0≤x1<x2≤1且|y1-y2|<2|x1-x2|=-2(x1-x2)(1)
又| y1-y2|=|f(x1)- f(x2)|= f(x1)- f(0)+ f(1)- f(x2)|
≤f(x1)- f(0)|+| f(1)- f(x2)|≤2|x1-0|+2|x2-1|=2(x1-0)+2(1-x2)=2(x1-x2)+2(2)
(1)+(2)得:
2|y1-y2|<2,
∴|y1-y2|<1(14分)
17、(本小题满分12分)本题考查互斥事件有一发生的概率和相互独立事件同时发生的概率,并考查分析问题解决问题的能力
解:分别记在这段时间内开关能够闭合为事件A、B、C,则它们的对立事件为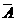 ,
,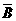 ,
,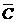 且P(A)=P(B)=P(C)=0.7,P(
且P(A)=P(B)=P(C)=0.7,P(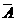 )=P(
)=P(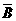 )=P(
)=P(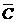 )=1-0.7=0.3根据题意在这段时间内3个开关是否能够闭合相互之间没有影响,即事件A、B、C相互独立(2分)
)=1-0.7=0.3根据题意在这段时间内3个开关是否能够闭合相互之间没有影响,即事件A、B、C相互独立(2分)
(1)在这段时间内“开关JA,JB恰有一个闭合”包括两种情况:一种是开关JA闭合但开关JB不闭合(事件A·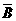 发生),一种是开关JA不闭合但开关JB闭合(事件
发生),一种是开关JA不闭合但开关JB闭合(事件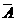 ·B发生),根据题意这两种情况不可能同时发生即事件A·
·B发生),根据题意这两种情况不可能同时发生即事件A·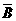 与事件
与事件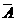 ·B互斥。根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率是:
·B互斥。根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率是:
P(A·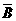 +
+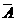 ·B)=P(A+
·B)=P(A+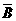 )+P(
)+P(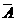 +B)=P(A)P(
+B)=P(A)P(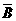 )+P(
)+P(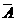 )P(B)
)P(B)
=0.7·0.3+0.3·0.7=0.42(7分)
(2)在这段时间内,线路正常工作,意味着3个开关至少有一个能够闭合,即事件A、B、C至少有一个发生,其对立事件为事件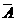 ,
,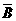 ,
,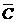 同时发生于是所求的概率为:
同时发生于是所求的概率为:
1-P(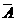 ·
·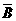 ·
·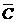 )=1-P(
)=1-P(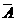 )P(
)P(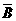 )P(
)P(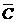 )=1-0.3·0.3·0.3=1-0.027=0.973(11分)
)=1-0.3·0.3·0.3=1-0.027=0.973(11分)
答:开关JA,JB恰有一个闭合的概率为0.42;线路正常工作的概率是0.973(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com