
题目列表(包括答案和解析)
7.点P在曲线y=x3-x+7上移动,过P点的切线的倾斜角取值范围是
A.[0,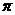
 B.(0,
B.(0,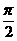 )∪[
)∪[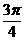 ,
, 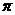

C.[0, 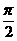
 ∪(
∪(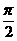 ,
,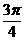
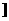 D.[0,
D.[0, 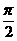
 ∪[
∪[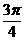 ,
, 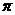 )
)
6.直线y=x+5与曲线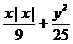 =1的交点的个数是
=1的交点的个数是
A.0 B.1
C.2 D.3
5.对于定义在实数集R上的函数f(x),如果存在实数x0,使f(x0)=x0,那么x0叫做函数f(x)的一个不动点.已知函数f(x)=x2+2ax+1不存在不动点,那么a的取值范围是
A.(-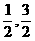 ) B.(-
) B.(- )
)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
4.给定两个向量a=(3,4),b=(2,1),若(a+xb)⊥(a-b),则x等于
A.-3 B.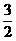
C.3 D.-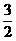
3.某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人.现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为
A.450 B.400
C.300 D.200
2.设复数z1=2-i,已知|z2|=|z1|,且arg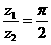 ,则复数z2的值为
,则复数z2的值为
A.1+2i B.1-2i
C.-1+2i D.-1-2i
1.对于函数f(x)=lgsinx(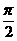 <x<
<x<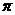
 ,下列说法中正确的是
,下列说法中正确的是
A.f(x)是增函数,且f(x)>0 B.f(x)是增函数,且f(x)<0
C.f(x)是减函数,且f(x)>0 D.f(x)是减函数,且f(x)<0
22.(本小题满分12分)
设函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2ax+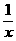 (a∈R).
(a∈R).
(1)当x∈(0,1]时,求f(x)的解析式;
(2)若a>-1,试判断f(x)在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值-6.
21. (本小题满分14分)
设椭圆 =1(a>b>0)的焦点为F1、F2,P是椭圆上任一点,若∠F1PF2的最大值为
=1(a>b>0)的焦点为F1、F2,P是椭圆上任一点,若∠F1PF2的最大值为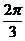 .
.
(1)求椭圆的离心率;
(2)设直线l与椭圆交于M、N两点且l与以原点为圆心,半径为短轴的圆相切.已知线段MN的长度最大值为4,求椭圆的方程与直线l的方程.
20.(本小题满分12分)
某家用电器厂根据其产品在市场上的销售情况,决定对原来以每件2000元出售的一种产品进行调价,并按新单价的八折优惠销售.结果每件产品仍可获得实际销售价20%的利润.已知该产品每件的成本是原销售价的60%.
(1)求调价后这种产品的新单价是每件多少元?让利后的实际销售价是每件多少元?
(2)为使今年按新单价让利销售后的利润总额不低于20万元,今年至少应销售这种产品多少件?(每件产品利润=每件产品的实际销售价-每件产品的成本价)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com