20．(本小题满分12分)

如图，已知三角形PAQ顶点P(－3，0)，点A在y轴上，点Q在x轴正半轴上，

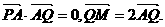
(Ⅰ)当点A在y轴上移动时，求动点M的轨迹E；

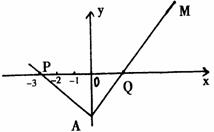　 (Ⅱ)设直线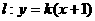与轨迹E交于B、C两点，点D(1，0)，若∠BDC为钝角，求k的取值范围.

19．(本小题满分12分)

如图：直平行六面体ABCD-A₁B₁C₁D₁,底面ABCD是边长为2a的菱形，∠BAD=60°，E为AB中点，二面角A₁-ED-A为60°.

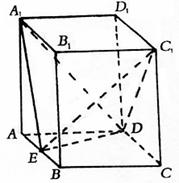　 (Ⅰ)求证：平面A₁ED⊥平面ABB₁A₁；

(Ⅱ)求二面角A₁-ED-C₁的余弦值.

(Ⅰ)根据比赛规则，高三(1)班代表队共可排出多少种不同的出场阵容？

(Ⅱ)高三(1)班代表队三盘比赛中两胜一负的概率是多少？

18．(本小题满分12分)

已知O为坐标原点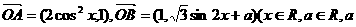，是常数)，若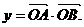

(Ⅰ)求y关于x的函数解析式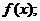

(Ⅱ)若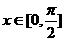时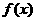，的最大值为2，求a的值并指出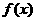的单调区间.

17．(本小题满分12分)

16．正△ABC的边长为3，D、E分别为BC边上的三等分点，沿AD，AE折起，使B、C两点重合于点P，则下列结论：①AP⊥DE；②AP与面PDE所成的角的正弦值是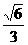；③P到平面ADE的距离为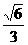；④AP与底面ADE所成的角为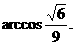其中正确的结论的序号为　　　　　　　 (把你认为正确的结论序号都填上).

15．一个口袋中装有大小相同的2个白球和3个黑球，从中摸出一个球，放回后再摸出一个球，则两次摸出的球恰好颜色不同的概率为　　　　　　　　 .

14．函数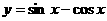的图象可以看成是由函数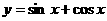的图象向右平移得到的，则平移的最小长度为　　　　　　 .

13．若A(6，m)是抛物线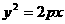上的点，F是抛物线的焦点，且|AF|=10，则此抛物线的焦点到准线的距离为　　　　　　 .

12．已知函数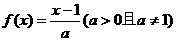，在同一直角坐标系中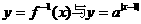，的图象可能是　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

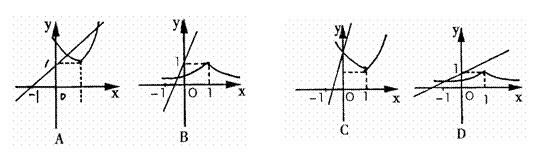
第Ⅱ卷(非选择题　 共90分)

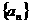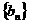11．由1，3，5，…，2n－1，…构成数列，数列满足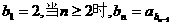，则b₅等于　　　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．63　　　　　　　　　　　 B．33　　　　　　　　　　　 C．17　　　　　　　　　　　 D．15