
题目列表(包括答案和解析)
6. 求椭圆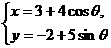 的中心坐标、焦点坐标、长轴和短轴的长,以及准线方程。
的中心坐标、焦点坐标、长轴和短轴的长,以及准线方程。
5.(选修4-2矩阵与变换)求矩阵A=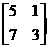 的逆矩阵.
的逆矩阵.
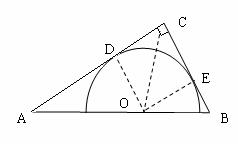
4.(选修4-1几何证明与选讲)半圆的圆心O在直角三角形ABC的斜边AB上,且半圆与两直角边相切.若斜边长为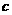 ,半圆半径为
,半圆半径为 ,求直角三角形的面积S.
,求直角三角形的面积S.
3. (选修4-5不等式选讲)已知a,b为正实数,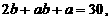 求函数
求函数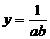 的最小值
的最小值
2.如图,在直角梯形OABC中,∠COA=∠OAB=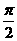 ,OC=2,OA=AB=1。SO⊥平面OABC,SO=1,以OC,OA,OS分别为x轴、y轴、z轴建立空间直角坐标系O-xyz。
,OC=2,OA=AB=1。SO⊥平面OABC,SO=1,以OC,OA,OS分别为x轴、y轴、z轴建立空间直角坐标系O-xyz。
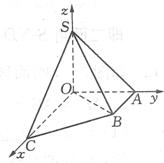 (Ⅰ)求
(Ⅰ)求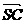 与
与 的夹角
的夹角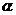 的余弦值;
的余弦值;
(Ⅱ)设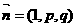 ,满足
,满足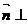 平面SBC,求
平面SBC,求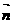 的坐标。
的坐标。
1.求曲线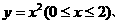 直线
直线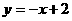 、
、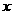 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
20.(16分)设A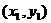 ,B
,B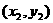 是函数
是函数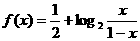 图象上任意两点,且
图象上任意两点,且
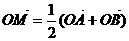 ,点M的横坐标为
,点M的横坐标为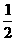 。
。
(Ⅰ)求证M点的纵坐标为定值;
(Ⅱ)若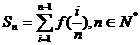 ,且
,且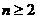 ,求
,求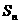 ;
;
(Ⅲ)已知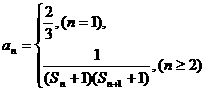 ,
,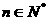 ,
,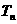 为数列
为数列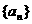 的前
的前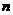 项和,
项和,
若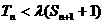 对于一切
对于一切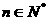 都成立,求
都成立,求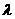 的取值范围。
的取值范围。
数学(选修物理学科)加试题
(总分40分)
(第1题和第2题为必做题;第3-6题选做2题;10分 4=40分)
4=40分)
19.(16分)某造船厂年最高造船量是20艘,已知造船x艘的产值函数为
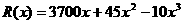 (单位:万元),成本函数为
(单位:万元),成本函数为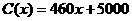 (单
(单
位:万元)。又在经济学中,函数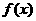 的边际函数
的边际函数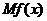 定义为:
定义为:
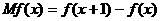 。求:
。求:
(Ⅰ)利润函数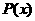 及边际利润函数
及边际利润函数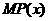 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)年造船量安排多少艘时,可使造船厂的年利润最大?
(Ⅲ)求边际利润函数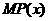 的单调递减区间,并说明单调递减在本题中的实际意义
的单调递减区间,并说明单调递减在本题中的实际意义
是什么?
18.(15分)已知f(x)=(x-1)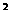 , g(x)=4(x-1),数列﹛an﹜中,对 任意正整数n,等
, g(x)=4(x-1),数列﹛an﹜中,对 任意正整数n,等
式(an+1-an)g(an)+f(an)=0都成立。且a1=2 当n≥2时 an≠1,设bn=an-1
(Ⅰ)求证数列﹛bn﹜是等比数列;
(Ⅱ)设Sn为数列﹛nbn﹜前n项和,Tn=Sn+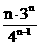 求Tn的取值范围。
求Tn的取值范围。
17.(15分)当实数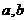 变化时,直线
变化时,直线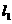 :
:
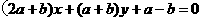 与直线
与直线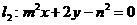 都过一个定点.
都过一个定点.
(Ⅰ)求出这个定点;
(Ⅱ)点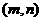 在怎样的曲线上?求出这条曲线的方程,并写出该曲线的焦点坐标.
在怎样的曲线上?求出这条曲线的方程,并写出该曲线的焦点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com