
题目列表(包括答案和解析)
19. (本题满分13分)
设双曲线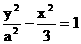 的焦点分别为
的焦点分别为 、
、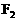 ,离心率为2。
,离心率为2。
(1)求此双曲线的渐近线l1、l2的方程;
(2)设A、B分别为l1、l2上的动点,且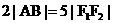 ,求线段AB中点M的轨迹方程,并说明是什么曲线。
,求线段AB中点M的轨迹方程,并说明是什么曲线。
18. (本题满分13分)
甲、乙两人进行5次比赛,如果甲或乙无论谁胜了3次,则宣告比赛结束。假定甲获胜的概率是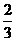 ,乙获胜的概率是
,乙获胜的概率是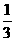 ,试求:
,试求:
(1)比赛以甲3胜1败而宣告结束的概率;
(2)比赛以乙3胜2败而宣告结束的概率;
(3)设甲先胜3次的概率为a,乙先胜3次的概率为b,求a:b。
17. (本题满分14分)
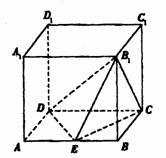
如图所示,在正方体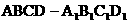 中,E为AB的中点。设正方体的棱长为2a。
中,E为AB的中点。设正方体的棱长为2a。
(1)求AD和B1C所成的角;
(2)证明:平面EB1D⊥平面B1CD;
(3)求二面角E-B1C-D的斜弦值。
16. (本题满分14分)
已知函数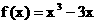
(1)求函数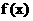 在
在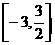 上的最大值和最小值;
上的最大值和最小值;
(2)过点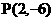 作曲线
作曲线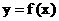 的切线,求此切线的方程。
的切线,求此切线的方程。
15. (本题满分13分)
在△ABC中,a,b,c分别是角A,B,C的对边,已知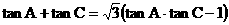 ,且
,且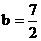 ,
,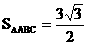 。求:
。求:
(1)角B;
(2)a+c的值。
14. 对于任意的两个实数对(a,b)和(c,d),规定: ,当且仅当a=c,b=d时成立。
,当且仅当a=c,b=d时成立。
运算“Ä”为:(a,b)Ä(c,d)=(ac-bd,bc+ad)
运算“Å”为:(a,b)Å(c,d)=(a+c,b+d)
现设p,q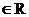 ,若(1,2)Ä(p,q)=(5,0),则(1,2)Å(p,q)=____________。
,若(1,2)Ä(p,q)=(5,0),则(1,2)Å(p,q)=____________。
13. 某人的电子邮箱的密码由5位数字组成,为提高保密程度,他决定再插入两个英文字母a,b,原来的数字及顺序不变,则可构成新密码的个数为________________个。
12. 已知数列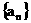 的首项
的首项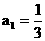 ,且满足
,且满足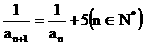 ,则
,则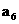 =______________。
=______________。
11. 不等式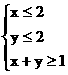 表示的平面区域的面积是____________________,
表示的平面区域的面积是____________________, 的最小值是_______________________。
的最小值是_______________________。
10. 设a、b都是单位向量,且a与b的夹角为60°,则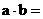 _________________,
_________________,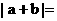 ______________________。
______________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com