
题目列表(包括答案和解析)
2.抛物线y=ax2的准线方程是y=1,则a的值为
A.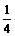 B.
B.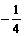 C.4
D.-4
C.4
D.-4
1.设集合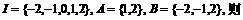 A∪(CIB)=
A∪(CIB)=
A.{1} B.{1,2} C.{2} D.{0,1,2}
22. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们用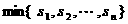 和
和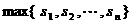 分别表示实数
分别表示实数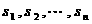 中的最小者和最大者.
中的最小者和最大者.
(1)设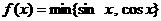 ,
,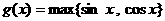 ,
, ,函数
,函数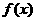 的值域为
的值域为 ,函数
,函数 的值域为
的值域为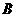 ,求
,求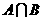 ;
;
(2)数学课上老师提出了下面的问题:设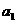 ,
,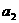 ,…,
,…,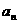 为实数,
为实数,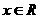 ,求函数
,求函数
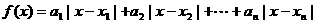 (
(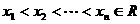 )的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
)的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数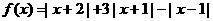 和
和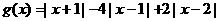 的最值.
的最值.
学生甲得出的结论是: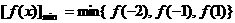 ,且
,且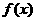 无最大值.
无最大值.
学生乙得出的结论是: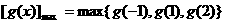 ,且
,且 无最小值.
无最小值.
请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
21. (本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
设椭圆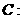
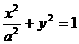 (
(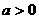 )的两个焦点是
)的两个焦点是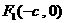 和
和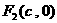 (
(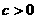 ),且椭圆
),且椭圆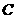 与圆
与圆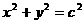 有公共点.
有公共点.
(1)求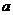 的取值范围;
的取值范围;
(2)(理)若椭圆上的点到焦点的最短距离为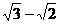 ,求椭圆的方程;
,求椭圆的方程;
(文)如果椭圆的两个焦点与短轴的两个端点恰好是正方形的四个顶点,求椭圆的方程;
(3)(理)对(2)中的椭圆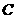 ,直线
,直线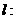
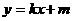 (
(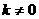 )与
)与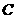 交于不同的两点
交于不同的两点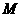 、
、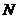 ,若线段
,若线段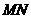 的垂直平分线恒过点
的垂直平分线恒过点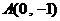 ,求实数
,求实数 的取值范围.
的取值范围.
(文)过(2)中椭圆右焦点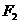 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线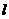 交椭圆于
交椭圆于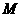 、
、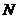 两点,线段
两点,线段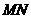 的垂直平分线与
的垂直平分线与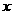 轴交于点
轴交于点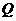 ,求点
,求点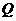 的横坐标的取值范围.
的横坐标的取值范围.
20. (本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.
甲、乙两公司生产同一种新产品,经测算,对于任意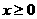 ,存在两个函数
,存在两个函数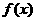 ,
, ,当甲公司投入
,当甲公司投入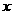 万元用于产品的宣传时,若乙公司投入的宣传费小于
万元用于产品的宣传时,若乙公司投入的宣传费小于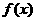 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入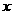 万元用于产品的宣传时,若甲公司投入的宣传费小于
万元用于产品的宣传时,若甲公司投入的宣传费小于 万元,则甲公司有失败的风险,否则无失败风险.
万元,则甲公司有失败的风险,否则无失败风险.
(1)解释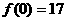 ,
,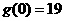 的实际意义;
的实际意义;
(2)当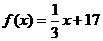 ,
,
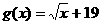 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
19.(本题满分14分) 本题共有2个小题,理科第1小题满分8分,第2小题满分6分;文科第1小题满分6分,第2小题满分8分.
如图,点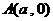 、
、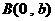 分别是
分别是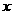 轴和
轴和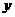 轴正半轴上的定点,动点
轴正半轴上的定点,动点 满足
满足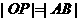 ,点
,点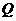 满足
满足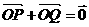 .
.
(理)(1)用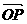 与
与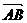 来表示
来表示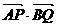 ;
;
(2)当向量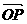 与
与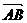 的夹角
的夹角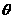 为何值时,
为何值时,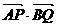 的值最大,并求出此最大值.
的值最大,并求出此最大值.
(文)(1)用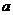 ,
,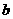 ,
,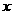 ,
,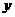 来表示
来表示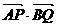 ;
;
(2)求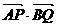 的最大值,并求出当
的最大值,并求出当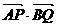 取最大值时点
取最大值时点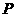 的坐标.
的坐标.
18. (本题满分12分)
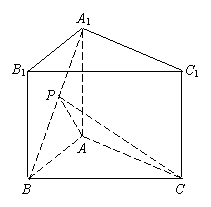 (理)在直三棱柱
(理)在直三棱柱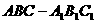 中,底面△
中,底面△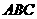 是等腰直角三角形,
是等腰直角三角形,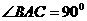 ,
, 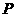 为
为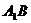 的中点,且
的中点,且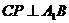 ,求二面角
,求二面角 的大小.
的大小.
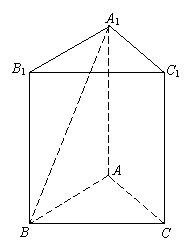 (文)底面边长为
(文)底面边长为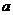 的正三棱柱的体积为
的正三棱柱的体积为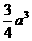 ,求异面直线
,求异面直线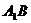 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
17. (本题满分12分)设 ,
,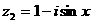 (
(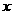 为实数且
为实数且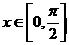 ,
,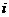 为虚数单位).
为虚数单位).
求函数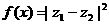 的值域.
的值域.
16.(理)若函数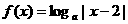 (
(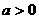 且
且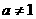 )在区间
)在区间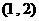 上是增函数,则
上是增函数,则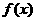
在区间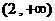 上为…………………………………………………………………( )
上为…………………………………………………………………( )
(A) 增函数且有最大值. (B) 增函数且无最大值
(C) 减函数且有最小值. (D) 减函数且无最小值.
(文)已知函数 (
(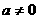 )在区间
)在区间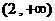 上是增函数,则函数
上是增函数,则函数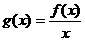 在区间
在区间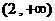 上的单调性为………………………………………( )
上的单调性为………………………………………( )
(A) 先减后增. (B) 先增后减. (C) 单调递减. (D) 单调递增.
15.制作一个面积为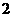
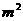 ,形状为直角三角形的钢框架,有下列四种长度的钢管可供选用,
,形状为直角三角形的钢框架,有下列四种长度的钢管可供选用,
则最合适(既够用,又剩余最少)的长度为……………………………………………( )
(A) 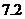
 .
(B)
.
(B) 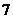
 .
(C)
.
(C) 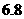
 .
(D)
.
(D) 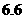
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com