
题目列表(包括答案和解析)
21.解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为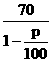 (11.8一户)万元,
(11.8一户)万元,
则商场该年对该商品征收的总管理费为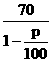 (11·8一p)p%(万元)
(11·8一p)p%(万元)
故所求函数为 y=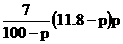
由11.8-p>0及p>0得定义域为0<p<11.8 ……………………………5分
(2) 由y≥14得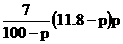 ≥14
≥14
化简得p2-12p+20≤0,即(p-2)(p-10)≤0,解得2≤p≤l0
故当比率为[2%,10%]内时,商场收取的管理费将不少于14万元.…8分
(3) 第二年,当商场收取的管理费不少于14万元时,
厂家的销售收入为g(p)= 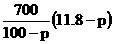 (2≤p≤10)
(2≤p≤10)
∵ g(p)= 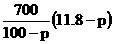 =700(10+
=700(10+ )为减函数,
)为减函数,
∴ g(p)max =g(2)=700(万元)
故当比率为2%时,厂家销售金额最大,且商场所收管理费又不少于14万元 ………………………12分
20.(本小题满分12分)
解:
(Ⅰ)
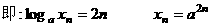 --------6分
--------6分
(Ⅱ)当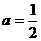 时,
时,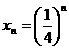
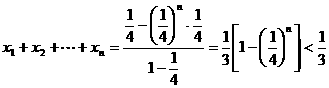 ----------12分
----------12分
19.解:(1)在直三棱柱ABC-A1B1C1中,
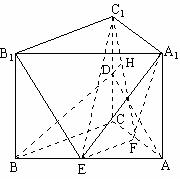 (1)∵
(1)∵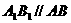 ,
,
∴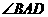 (或其补角)为异面直线AD与A1B1所成的角,
(或其补角)为异面直线AD与A1B1所成的角,
………………………2分,连结BD,
在 中,∵AC=4,
中,∵AC=4,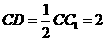
∴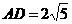 ,
,
在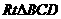 中,∵BC=3,CD=2,∴
中,∵BC=3,CD=2,∴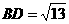 ,
,
在△ABD中,∵AB=5,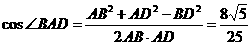
∴异面直线AD与A1B1所成角的余弦值为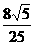 ………………………………4分
………………………………4分
(2)证明:∵AB=5,BC=3,AC=4,∴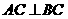 ,
,
∵底面ABC⊥侧面ACC1A1,∴BC⊥侧面ACC1A1,………………………………6分
取AB、AC的中点E、F,连结EF、A1F,则EF//BC,
∴EF⊥平面ACC1A1, ∴A1F为A1E在侧面AC1内的射影,
在正方形C1CAA1内,∵ D、F分别为CC1、AC的中点,
∴ ≌
≌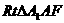 ,∴
,∴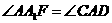 ,
,
∴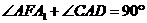 ,∴
,∴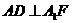 ,
,
∴ (三垂线定理)………………8分
(三垂线定理)………………8分
(3)连结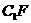 ,过D作DH⊥
,过D作DH⊥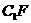 ,垂足为H。
,垂足为H。
∵EF//BC,BC//B1C1,∴EF// B1C1,∴点F在平面B1C1E内。
∵EF⊥平面ACC1A1,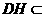 平面ACC1A1,EF⊥DH,………………10分
平面ACC1A1,EF⊥DH,………………10分
∵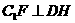 ,
,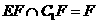 ,∴DH⊥平面B1C1E。
,∴DH⊥平面B1C1E。
在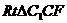 中,∵
中,∵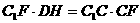 ,∴
,∴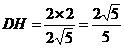 。……………12分
。……………12分
(本题用空间向量法来解,每小题对应给分)
18、解 (1)由题意得a<0且ax2+(b-8)x-a-ab=0的根为-3,2……………2分
-3+2=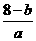 ,(-3)×2=
,(-3)×2=
 ,从而a=-3,b=5……………………4分
,从而a=-3,b=5……………………4分
f(x)=-3x2-3x+18,对称轴为x=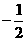 ,可得f(x)∈[12,18]
………………7分
,可得f(x)∈[12,18]
………………7分
(2)由-3x2+5x+c≤0得c≤3x2-5x恒成立,得c≤-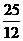 …………………… 12分
…………………… 12分
17. (1)由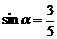 得
得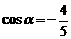 ……………………………… 2分
……………………………… 2分
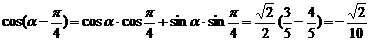 …………6分
…………6分
(2)原式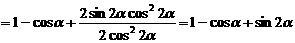
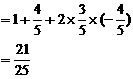 ……………………12分
……………………12分
13. 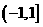 ; 14.
; 14. 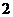 ; 15. 11 ; 16. ② ③
; 15. 11 ; 16. ② ③
|
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10. |
11. |
12. |
|
A |
B |
B |
C |
C |
A |
D |
B |
C |
B |
C |
D |
22.(本小题满分14分)  是以
是以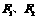 为焦点的双曲线C:
为焦点的双曲线C: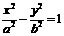 (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知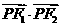 =0,
=0,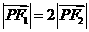 .(1)试求双曲线的离心率
.(1)试求双曲线的离心率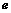 ;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当
;(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当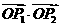 =-
=- ,
,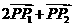 =
=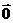 ,求双曲线的方程.
,求双曲线的方程.
高三文科数学第一学期期末联考
21.(本小题满分12分)
某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件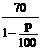 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2) 要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3) 第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
20.(本小题满分12分)
设函数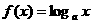 (
( ),已知数列
),已知数列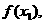

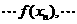 是公差为2的等差数列,且
是公差为2的等差数列,且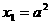 .
.
(Ⅰ)求数列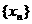 的通项公式;
的通项公式;
(Ⅱ)当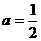 时,求证:
时,求证: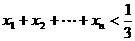 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com