
题目列表(包括答案和解析)
8.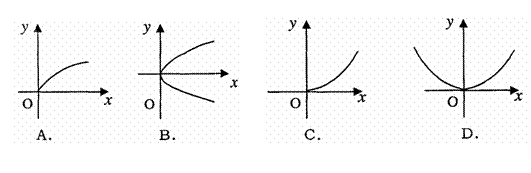 已知
已知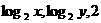 成等差数列,则M(x,y)的轨迹为 ( )
成等差数列,则M(x,y)的轨迹为 ( )
7.设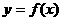 为可导的奇函数,且
为可导的奇函数,且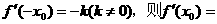 ( )
( )
A.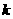 B.
B.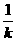 C.-
C.-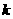 D.-
D.-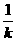
6.已知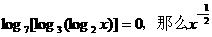 等于 ( )
等于 ( )
A.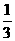 B.
B.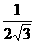 C.
C.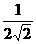 D.
D.
5.圆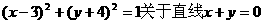 对称的圆的方程是 ( )
对称的圆的方程是 ( )
A.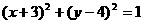 B.
B.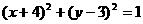
C.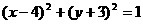 D.
D.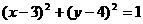
4.将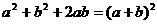 改写成全称命题是 ( )
改写成全称命题是 ( )
A.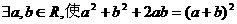
B.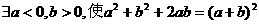
C.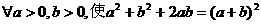
D.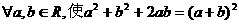
3.问题:①某社区有500个家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解购买力的某项指标,要从中抽出一个容量为100户的样本;②从10名学生中抽出3人参加座谈会。
方法:Ⅰ随机抽样法;Ⅱ系统抽样法;Ⅲ分层抽样法。
问题与方法配对正确的是 ( )
A.①Ⅲ,②Ⅰ B.①Ⅰ,②Ⅱ C.①Ⅱ,②Ⅲ D.①Ⅲ,②Ⅱ
2.设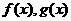 是定义在R上的函数,
是定义在R上的函数,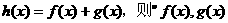 均为偶函数”是“
均为偶函数”是“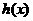 为偶函数”的 ( )
为偶函数”的 ( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分又不必要条件
1.设集合M={-1,0,1},N={a,a2},则使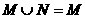 成立的a的值是 ( )
成立的a的值是 ( )
A.-1 B.0 C.1 D.-1或1
22.(1)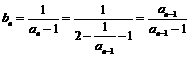 ,而
,而 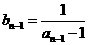 ,
,
∴ 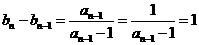 .
.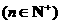
∴ {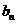 }是首项为
}是首项为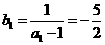 ,公差为1的等差数列.…………… 4分
,公差为1的等差数列.…………… 4分
(2)由(1)有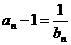 ,而
,而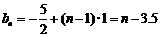 , ∴
, ∴ 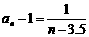 .对于函数
.对于函数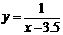 ,在x>3.5时,y>0,
,在x>3.5时,y>0,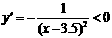 ,在(3.5,
,在(3.5, )上为减函数.
)上为减函数.
故当n=4时,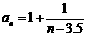 取最大值3. ……………………………… 6分
取最大值3. ……………………………… 6分
而函数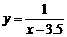 在x<3.5时,y<0,
在x<3.5时,y<0,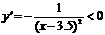 ,在(
,在(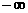 ,3.5)上也为减函数.故当n=3时,取最小值,
,3.5)上也为减函数.故当n=3时,取最小值,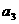 =-1. ……………………………………… 8分
=-1. ……………………………………… 8分
(3)
用数学归纳法证明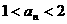 ,再证明
,再证明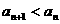
① 当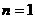 时,
时,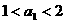 成立; ……………………………………… 9分
成立; ……………………………………… 9分
②假设当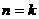 时命题成立,即
时命题成立,即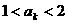 ,
,
当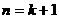 时,
时,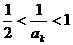
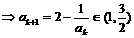
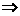
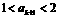
故当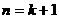 时也成立, ……………………………………… 11分
时也成立, ……………………………………… 11分
综合①②有,命题对任意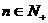 时成立,即
时成立,即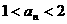 . …………12分
. …………12分
(也可设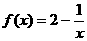 (1≤
(1≤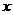 ≤2),则
≤2),则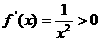 ,
,
故
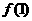
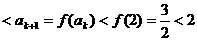 ).
).
下证: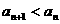
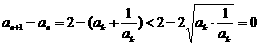
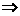
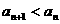 .………………………14分
.………………………14分
(本小题若不用数学归纳法证明,需对应给分。)
21.解(1)∵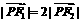 ,
,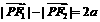 ,∴
,∴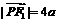 ,
,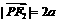 .
.
∵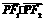 =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴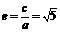 .…………………4分
.…………………4分
(2)由(1)知,双曲线的方程可设为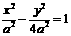 ,渐近线方程为
,渐近线方程为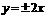 .……5分
.……5分
设P1(x1,2x1),P2(x2,-2x2),P(x,y).………………………………………6分
∵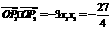 ,∴
,∴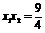 . ∵
. ∵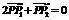 ,∴
,∴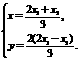 …………10分
…………10分
∵点P在双曲线上,∴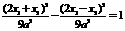 .
.
化简得,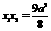 .∴
.∴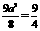 .∴
.∴ 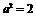 .∴双曲线的方程为
.∴双曲线的方程为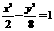 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com