
题目列表(包括答案和解析)
8.有5人排成一排照相,其中甲、乙两人必须相邻且不排在两头,则不同的排法共有
(A) 12种 (B) 18种 (C) 24种 (D) 36种
7.若 展开式的第5项等于
展开式的第5项等于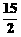 ,则x的值是
,则x的值是
(A)2 (B)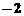 (C)
(C)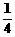 (D)
(D)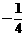
6.已知直线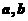 ,平面
,平面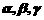 ,则使
,则使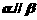 成立的一个充分条件是
成立的一个充分条件是
(A) (B)
(B)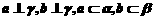
(C)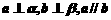 (D)
(D)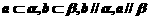
5.已知A、B、C三点共线(该直线不过原点O),若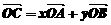 ,则
,则
(A)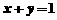 (B)
(B)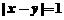 (C)
(C)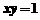 (D)
(D)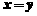
4.函数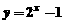 的图像是
的图像是

3.某中学有高一学生400人,高二学生300人,高三学生500人,现用分层抽样的方法在这三个年级中抽取120人进行体能测试,则从高三抽取的人数应为
(A)40 (B)48 (C)50 (D)80
2.计算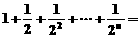
(A)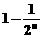 (B)
(B)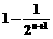 (C)
(C)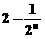 (D)
(D)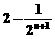
1.设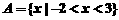 ,
, ,则
,则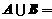
(A)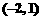 (B)
(B)
(C) (D)
(D)
21.(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数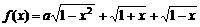 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=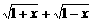 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足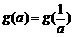 的所有实数a
的所有实数a
解:本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力。
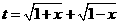
要使有t意义,必须1+x≥0且1-x≥0,即-1≤x≤1,
∴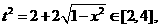 t≥0
①
t≥0
①
t的取值范围是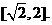 由①得
由①得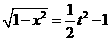
∴m(t)=a(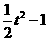 )+t=
)+t=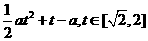
(2)由题意知g(a)即为函数 的最大值。
的最大值。
注意到直线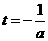 是抛物线
是抛物线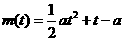 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
当a>0时,函数y=m(t), 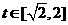 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由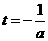 <0知m(t)在
<0知m(t)在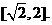 上单调递增,∴g(a)=m(2)=a+2
上单调递增,∴g(a)=m(2)=a+2
(2)当a=0时,m(t)=t, 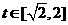 ,∴g(a)=2.
,∴g(a)=2.
(3)当a<0时,函数y=m(t), 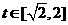 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若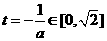 ,即
,即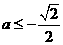 则
则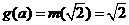
若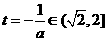 ,即
,即 则
则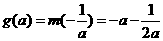
若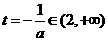 ,即
,即 则
则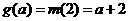
综上有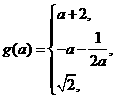
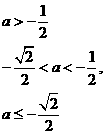
(3)解法一:
情形1:当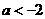 时
时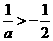 ,此时
,此时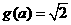 ,
,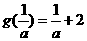
由 ,与a<-2矛盾。
,与a<-2矛盾。
情形2:当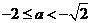
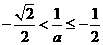 时,此时
时,此时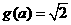 ,
,
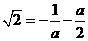 解得,
解得, 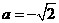 与
与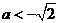 矛盾。
矛盾。
情形3:当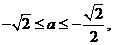
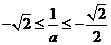 时,此时
时,此时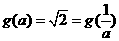
所以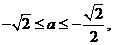
情形4:当 时,
时,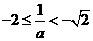 ,此时
,此时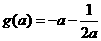 ,
,

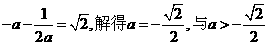 矛盾。
矛盾。
情形5:当 时,
时,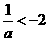 ,此时g(a)=a+2,
,此时g(a)=a+2,

由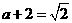 解得
解得 矛盾。
矛盾。
情形6:当a>0时, ,此时g(a)=a+2,
,此时g(a)=a+2, 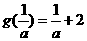
由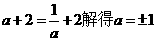 ,由a>0得a=1.
,由a>0得a=1.
综上知,满足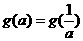 的所有实数a为
的所有实数a为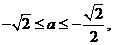 或a=1
或a=1
20.(本题满分14分,第1小题满分6分,第二小题满分8分)已知函数f(x)=x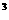 + x
+ x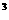 ,数列|x
,数列|x |(x
|(x >0)的第一项x
>0)的第一项x =1,以后各项按如下方式取定:曲线x=f(x)在
=1,以后各项按如下方式取定:曲线x=f(x)在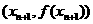 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x ,f (x
,f (x ))两点的直线平行(如图)
))两点的直线平行(如图)
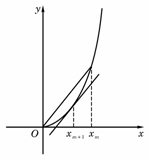 .
.
求证:当n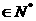 时,
时,
(Ⅰ)x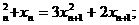
(Ⅱ)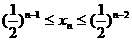
解:本题主要考查函数的导数、数列、不等式等基础知识,以及不等式的证明,同时考查逻辑推理能力。
证明:(I)因为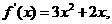
所以曲线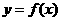 在
在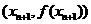 处的切线斜率
处的切线斜率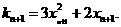
因为过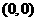 和
和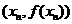 两点的直线斜率是
两点的直线斜率是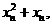
所以 .
.
(II)因为函数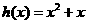 当
当 时单调递增,
时单调递增,
而
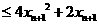
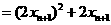 ,
,
所以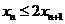 ,即
,即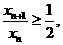
因此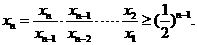
又因为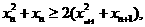
令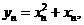
则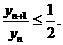
因为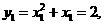
所以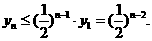
因此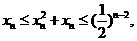
故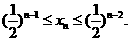
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com