2.已知抛物线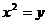，则它的准线方程为(　　 )

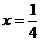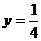A　　 　　　B　 　　　　C　　 　　D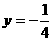　

1.设全集U={1，3，5，7}，集合A={3，5}，B={1，3，7}，则等于( 　)

A．{5}　　　　　 B．{3，5}　　　　 C．{1，5，7} 　　　 D．{1，3，5，7}

20.已知f(x)=ax³+bx²+cx+d(a≠0)是定义在R上的函数，其图象交x轴于A、B、C三点，若点B的坐标为(2，0)且f(x)在[-1,0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性

(1)求实数c的值；

(2)在函数f(x)图象上是否存在一点M(x₀,y₀)，使f(x)在点M的切线斜率为3b？若存在，求出点M的坐标；不存在说明理由

19.已知点A(-5，0)，B(5，0)，动点P满足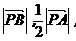8成等差数列

　 (1)求点P的轨迹方程；

　 (2)对于x轴上的点M，若满足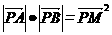，则称点M为点P对应的“比例点”，求证：对任意一个确定的点P，它总对应两个“比例点”.

　 (3)当点P在(1)的轨迹上运动时，求它在(2)中对应的“比例点”M的横坐标的取值范围。

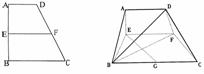
18.已知梯形ABCD中，AD∥BC，∠ABC=∠BAD=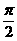，AB=BC=2AD=4，EF分虽是AB、CD上的点，EF∥BC，AE=x，G是BC的中点。沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF(如图)。

　 (1)当x=2时，求证：BD⊥EG；

　 (2)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值；

　 (3)当f(x)取得最大值时，求二面角D-BF-C的正切值.

17.某商家进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为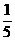，若中奖商家返还顾客现金1000多元。小王购买一套价格为2400元的西服，只能得到2张奖券，于是小王补偿50元给一同事购买一件价格为600元的便服，这样小王就得到了3张奖券。设小王这次消费的实际支出为ζ(元)

(1)求ζ的所有可能取值；

(2)求ζ的分布列；

(3)求Eζ；

(4)试说明小王出资50元增加1张奖券是否划算？

16.已知数列{a_n}的首项a₁=1，其前n项和为S_n，且对任意正整数n,有n,a_n,S_n成等差数列

　 (1)求证：数列{S_n+n+2}成等比数列.

　 (2)求数列{a_n}的通项公式.

15.已知二次项系为m(m≠0)的二次函数f(x)对任意x∈R,都有f(1-x)=f(1+x)成立，设向量a=(sinx,2),b=)(2sinx,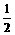),c=(cos2x,1),d=(1,2).

　 (1)分别求a·b和c·d的取值范围；

　 (2)当x∈[0，π]时，求不等式f(a·b)>f(c·d)的解集.

14.某种细胞开始时有2个，一小时后分裂成4个并死去1个，两小时后分裂成6个并死去1个，三个小时后分裂成10个并死去1个，……按照这种规律进行下去，100小时后细胞的存活数是　　 .

13.已知函数f(x)的图象是两条直线的一部分，其定义域为

　 [-1,0]∪(0,1),则不等式f(x)-f(-x)>-1的解集是　　 .