1、已知集合P={x|x²–9<0}，Q={x|x²–1>0}，则　　　 。

3．如图，正三棱柱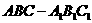的底面边长为a，点M在边BC上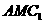，△是以点M为直角顶点的等腰直角三角形．

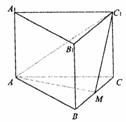
　(1)求证点M为边BC的中点；

　(2)求点C到平面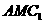的距离；

　(3)求二面角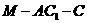的大小．

2．如图，直四棱柱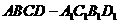的侧棱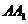的长是a，底面ABCD是边长AB=2a，BD=a的矩形，E为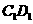的中点。　　　　　　　

(.1)求二面角E-BD-C的大小;

(2)求三棱锥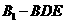的体积.　　　

1．正三棱锥P－ABC的底面边长为a，E、F分别是侧棱PB、PC的中点，且E、A、F三点的截面垂直于侧面PBC．

(1) 求棱锥的全面积；(2) 侧面与底面所成的角的余弦值．

4.在棱长为a的正方体ABCD-A₁B₁C₁D₁中，E、F分别是BC、A₁D₁的中点.

　　　 (1)求证：四边形B₁EDF是菱形；

(2)求直线A₁C与DB的距离；

(3)求直线AD与平面B₁EDF所成的角.

(4)求平面B₁D₁C与A₁DB的距离

5多　面　体

例1．斜三棱柱ABC-A₁B₁C₁的底面是边长为a的正三角形，侧棱长为b，

侧棱AA₁和AB、AC都成45°的角，求棱柱的侧面积和体积.

例2．三棱锥各侧面与底面均成45°角，底面三角形三内角A、B、C满足2B＝A+C，最大边与最小边是方程3x²－27x+32=0的两根．

(1)求棱锥的高；(2) 求棱锥的侧面积．

例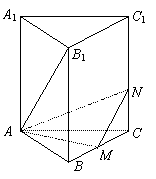3．如图，正三棱柱ABC-A₁B₁C₁的所有棱长都为4，M是BC的中点，N是CC₁上一点，满足MN⊥AB₁

(1)试求三棱锥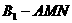的体积；

(2)求点C₁到平面AMN的距离。

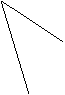
例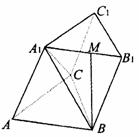4．如图，三棱柱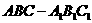的底面是边长为a的正三角形，侧面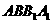是菱形且垂直于底面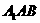，∠＝60°，M是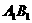的中点．

(1)求证：BM⊥AC；

(2)求二面角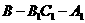的正切值；

(3)求三棱锥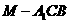的体积．

习题

3.如图，正三棱柱ABC-A₁B₁C₁的九条棱均相等，D是BC上一点，AD⊥C₁D.

(1).求证：截面ABC₁⊥侧面BCC₁B₁.

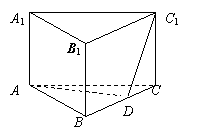(2)求二面角C-AC₁-D的大小.

(3)若AB=2，求直线A₁B与截面ADC₁的距离.

.

2.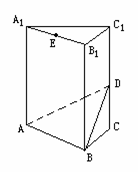如图，正三棱柱A₁B₁C₁-ABC中，底面边长和侧棱长都是1，D、E分别是C₁C和A₁B₁的中点．

(1)求点E到平面ABD的距离：

(2)求二面角A-BD-C的正切值．

4.在三棱锥S-ABC中，已知SA=4，AB=AC，BC=3,∠SAB=∠SAC=45º,SA与底面ABC所成的角为30º.

(1)求证：SA⊥BC；

(2)求二面角S-BC-A的大小;

(3)求三棱锥S-ABC的体积．

答案：(3)9

4　距离

　 例1、如图，直三棱柱ABC-A₁B₁C₁的底面ABC为等腰直

角三角形，∠ACB=90⁰，AC=1，C点到AB₁的距离为

CE=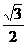，D为AB的中点.

(1)求证：AB­₁⊥平面CED；

(2)求异面直线AB₁与CD之间的距离；

(3)求二面角B₁-AC-B的平面角.

解:(1)∵D是AB中点，△ABC为等腰直角三角形，

∠ABC=90⁰，∴CD⊥AB又AA₁⊥平面ABC，∴CD⊥AA₁.

∴CD⊥平面A₁B₁BA　 ∴CD⊥AB₁，又CE⊥AB₁，

　∴AB₁⊥平面CDE；

(2)由CD⊥平面A₁B₁BA　 ∴CD⊥DE

∵AB₁⊥平面CDE　 ∴DE⊥AB_1,

∴DE是异面直线AB₁与CD的公垂线段

∵CE=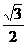，AC=1 , ∴CD=∴；

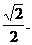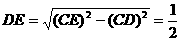(3)连结B₁C，易证B₁C⊥AC，又BC⊥AC ,

∴∠B₁CB是二面角B₁-AC-B的平面角.

在Rt△CEA中，CE=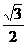，BC=AC=1,∴∠B₁AC=60⁰

∴，　 ∴,

∴ 　, ∴.

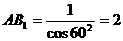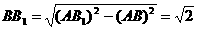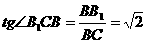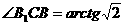例2、如图，正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直。点M在AC上移动，点N在BF上移动，若CM=BN=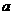

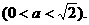
(1)　　　 求MN的长；

(2)　　　 当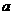为何值时，MN的长最小；

(3)　　　 当MN长最小时，求面MNA与面MNB所成的二面角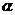的大小。

例3. 如图，平面a∩平面b＝MN，　　　　　　　　　　　

　　 二面角A－MN－B为60°,点A∈a，

　B∈b，C∈MN，∠ACM＝∠BCN＝45°.

　　 AC＝1,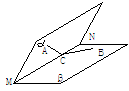

　　 (1) 求点A到平面b的距离；

　　 (2) 求二面角A－BC－M的大小．　　　

答案(1)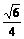； (2)arctan(提示：求出点A在平面 b 的射影到直线BC的距离为).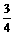

例4、已知直三棱柱ABC－A₁B₁C₁的侧棱AA₁＝4cm，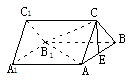

　 它的底面△ABC中有AC＝BC＝2cm，∠C＝90°,E是AB的

　 中点．

　 (1) 求证：CE和AB₁所在的异面直线的距离等于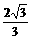cm；　

　 (2) 求截面ACB₁与侧面ABB₁A₁所成的二面角的大小．

答案 (2) arccos.

练习：1.已知：如图，△ABC中，AB=6cm，AC=8cm，BC=10cm，P是平面ABC外一点，且PA=PB=PC=6cm．

(1)求点P到平面ABC的距离；

(2)求PA与平面ABC所成角的余弦．

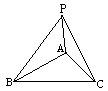
3.如图,四棱锥P-ABCD中，底面ABCD是边长为a的正方形，PD=a，PA=PC=a，

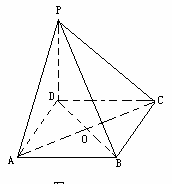(1)求证：PD⊥平面ABCD；

(2)求异面直线PB与AC所成角的大小；

(3)求二面角A-PB-D的大小；

(4)在这个四棱锥中放入一个球，求球的最大半径．

答案：(2)90°(3)60°(4)(2-√2)a/2

2..如图，正三棱柱ABC-A₁B₁C₁的底面边长为2，侧棱长为，D,E分别为AA₁,B₁C₁的中点.

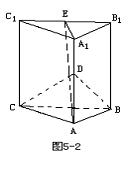(1)求证：平面AA₁E⊥平面BCD；

(2)求直线A₁B₁与平面BCD所成的角．

答案：(2)30°