
题目列表(包括答案和解析)
21、(本大题18分)
(1)已知平面上两定点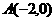 、
、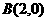 ,且动点M标满足
,且动点M标满足 =0,求动点
=0,求动点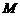 的轨迹方程;
的轨迹方程;
(2)若把(1)的M的轨迹图像向右平移一个单位,再向下平移一个单位,恰与直线x+ky–3=0 相切,试求实数k的值;
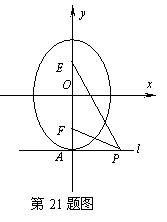 (3)如图,l是经过椭圆
(3)如图,l是经过椭圆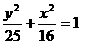 长轴顶点A且与长轴垂直的直线,E、F是两个焦点,点PÎl,P不与A重合。若ÐEPF=
长轴顶点A且与长轴垂直的直线,E、F是两个焦点,点PÎl,P不与A重合。若ÐEPF=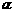 ,求
,求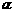 的取值范围。
的取值范围。
并将此题类比到双曲线: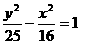 ,
, 是经过焦点
是经过焦点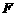 且与实轴垂直的直线,
且与实轴垂直的直线,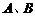 是两个顶点,点PÎl,P不与
是两个顶点,点PÎl,P不与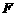 重合,请作出其图像。若
重合,请作出其图像。若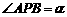 ,写出角
,写出角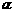 的取值范围。(不需要解题过程)
的取值范围。(不需要解题过程)
19、(本大题16分)
设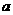 为实数,函数f(x)=x|x–a|,其中xÎR。
为实数,函数f(x)=x|x–a|,其中xÎR。
(1)分别写出当a=0、a=2、a= –2时函数f(x)的单调区间;
(2)判断函数f(x)的奇偶性,并加以证明。
18、(本大题14分)
在△ABC中,A为锐角,a=30,ΔABC的面积S=105,外接圆半径R=17。
(1)求sinA、cosA的值;(2)求ΔABC的周长。
17、(本大题12分)
复数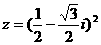 是一元二次方程
是一元二次方程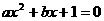
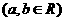 的根,
的根,
(1)求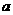 和
和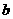 的值;(2)若
的值;(2)若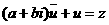
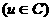 ,求
,求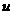 。
。
16、(本大题12分)
设函数f(x)=
–cos2x–4tsin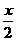 cos
cos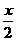 +2t2–3t+4,xÎR,其中|t|≤1,将f(x)的最小值记为g(t)。(1)求函数g(t)的表达式;(2)判断g(t)在[–1, 1]上的单调性,并求出g(t)的最值。
+2t2–3t+4,xÎR,其中|t|≤1,将f(x)的最小值记为g(t)。(1)求函数g(t)的表达式;(2)判断g(t)在[–1, 1]上的单调性,并求出g(t)的最值。
15、方程|x–2| = log 2x的解的个数为 ( )
(A) 0 (B) 1 (C) 2 (D) 3
14、已知A(1,0)、B(7,8),若点 和点
和点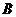 到直线l的距离都为5,且满足上述条件的直线l共有n条,则n的值是
( )
到直线l的距离都为5,且满足上述条件的直线l共有n条,则n的值是
( )
(A) 1 (B) 2 (C) 3 (D) 4
13、命题:“对任意的 ,
,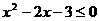 ”的否定是
( )
”的否定是
( )
(A)不存在 ,
,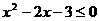 ; (B)存在
; (B)存在 ,
,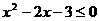 ;
;
(C)存在 ,
,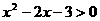 ; (D)对任意的
; (D)对任意的 ,
,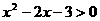 .
.
12、在复平面内,复数z=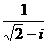 对应的点位于
( )
对应的点位于
( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com