
题目列表(包括答案和解析)
19.(本小题满分14分,第一小问满分3分,第二小问满分5分,第三小问满分6分)
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=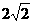 a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
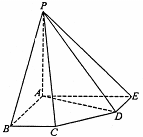 (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的大小;
(3)求点C到平面PDE的距离. (南菁中学)
解:(1)证明∵PA=AB=2a,PB=2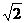 a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
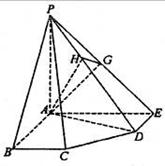 同理PA⊥AE.3分∵AB∩AE=A,∴PA⊥平面ABCDE. …………… 3分
同理PA⊥AE.3分∵AB∩AE=A,∴PA⊥平面ABCDE. …………… 3分
(2)∵∠AED=90°,∴AE⊥ED.
∵PA⊥平面ABCDE,∴PA⊥ED.
∴ED⊥平面PAE.过A作AG⊥PE于G,
∴DE⊥AG,∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. ………… 6分
在直角△PAE中,AG=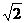 a.在直角△PAD中,AH=
a.在直角△PAD中,AH=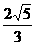 a,
a,
∴在直角△AHG中,sin∠AHG=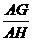 =
= .∴∠AHG=arcsin
.∴∠AHG=arcsin .
.
∴二面角A-PD-E的大小为arcsin . …………… 8分
. …………… 8分
(3)∵∠EAB=∠ABC=∠DEA=90°, BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC, ∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE, ∴CF∥DE,而DE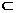 平面PDE,CF
平面PDE,CF 平面PDE,
平面PDE,
∴CF∥平面PDE.
∴点C到平面PDE的距离等于F到平面PDE的距离. ……………10分
∵PA⊥平面ABCDE, ∴PA⊥DE. 又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.
∴过F作FG⊥PE于G,则FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离. ……………12分
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
∴FG=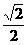 a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为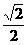 a.
…………… 14分
a.
…………… 14分
18.(本小题满分14分,第1小题满分6分,第二小题满分8分,)在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:
(1)乙连胜四局的概率;(2)丙连胜三局的概率.
解:(1)当乙连胜四局时,对阵情况如下:
第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
所求概率为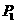 =
=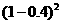 ×
×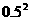 =
=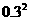 =0.09
=0.09
∴ 乙连胜四局的概率为0.09.-----------------------------------------------------6分
(2)丙连胜三局的对阵情况如下:
第一局:甲对乙,甲胜,或乙胜.
当甲胜时,第二局:甲对丙,丙胜.第三局:丙对乙,丙胜;第四局:丙对甲,丙胜.
当乙胜时,第二局:乙对丙,丙胜;第三局:丙对甲,丙胜;第四局:丙对乙,丙胜.
故丙三连胜的概率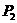 =0.4×
=0.4× ×0.5+(1-0.4)×
×0.5+(1-0.4)×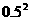 ×0.6=0.162.--------14分
×0.6=0.162.--------14分
17.(本小题满分12分, 第1小题满分5分,第二小题满分7分)在锐角三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,且 (成都)
(成都)
(I)若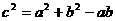 ,求A、B、C的大小;
,求A、B、C的大小;
(II)已知向量 的取值范围.
的取值范围.
解:由已知

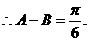 …………………………………………………………3分
…………………………………………………………3分
(I)由已知
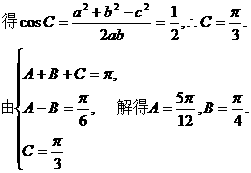
 ……………………………………………………3分
……………………………………………………3分
(II)|3m-2n|2=9 m 2+4n2-12 m·n =13-12(sinAcos B +cosAsin B)
=13-12sin(A+B)=13-12sin(2 B +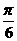 ).………………………3分
).………………………3分
∵△ABC为锐角三角形,A-B=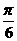 ,
,
∴C=π-A-B<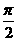 ,A=
,A=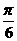 +B<
+B<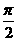 .
.

 …………………………………………………………2分
…………………………………………………………2分
∴|3m-2n|2=∈(1,7).
∴|3m-2n|的取值范围是(1,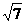 ).…………………………………………1分
).…………………………………………1分
16.已知映射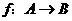 ,其中
,其中 ,对应法则
,对应法则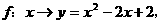 若对实数
若对实数 ,在集合A中不存在原象,则
,在集合A中不存在原象,则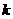 的取值范围是
的取值范围是 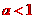 ;
;
15.已知函数 的值为_____
的值为_____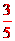 __________.
__________.
14.设函数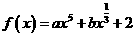 在区间
在区间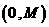 上的最大值为8,则
上的最大值为8,则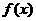 在区间
在区间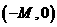 上的最小值为________-4________.
上的最小值为________-4________.
13. 将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .
将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .
12.已知d为抛物线y=2ax2(a>0)的焦点到准线的距离,则ad的值等于 
11.设a,b为实数,集合M={ ,1},N={a,0},f
: x
,1},N={a,0},f
: x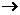 x表示集合M的元素x映射到集合N中仍为x,则a+b= 1
x表示集合M的元素x映射到集合N中仍为x,则a+b= 1
10. 如右图所示,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.点M为平面ABCD内的一个动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( A )
如右图所示,△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD.点M为平面ABCD内的一个动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( A )
第Ⅱ卷(非选择题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com