
题目列表(包括答案和解析)
3.(本大题满分12分)已知10件产品中有3件是次品. (1)任意取出3件产品作检验,求其中至少有1件是次品的概率; (2)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
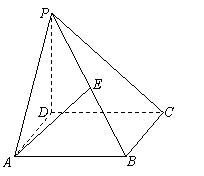
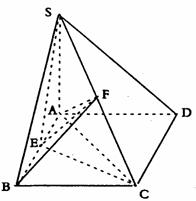
2.(本大题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD = AB = a,E是PB的中点,F为AD中点. (1)求异面直线PD、AE所成的角; (2)求证:EF⊥平面PBC. (3)求二面角F-PC-E的大小.
1.(本大题满分12分)设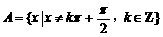 ,已知
,已知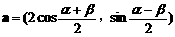 ,
,
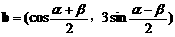 ,其中
,其中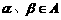 .(1)若
.(1)若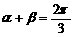 ,且a = 2b,求
,且a = 2b,求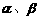 的值;
(2)若
的值;
(2)若 ,求
,求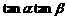 的值.
的值.
21.解:(I)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费。………………………………4分
(Ⅱ)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
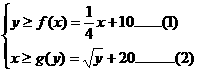 成立,双方均无失败的风险……………………8分
成立,双方均无失败的风险……………………8分
由(1)(2)得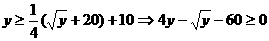
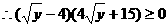
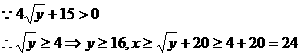

答:要使双方均无失败风险,甲公司至少要投入24万元,乙公司至少要投入16万元。………12元
20.解证:(I)易得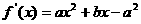 …………………………………………1分
…………………………………………1分
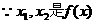 的两个极值点
的两个极值点 的两个实根,又a>0
的两个实根,又a>0
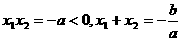 ……………………………………………………3分
……………………………………………………3分
∴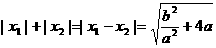 ∵
∵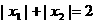
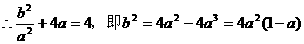
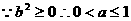 ……7分
……7分
(Ⅱ)设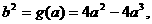 则
则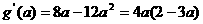
由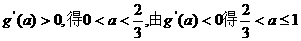
 上单调递增………………10分
上单调递增………………10分
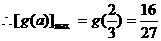
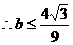 ………………………………………………12分
………………………………………………12分
19.解证:(Ⅰ)由题意知Sn=2an-3n
∴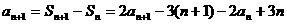
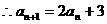 ………………2分
………………2分
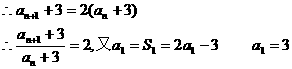 ∴a1+3=6……………4分
∴a1+3=6……………4分
∴数列{an+3}成以6为首项以2为公比的等比数列
(Ⅱ)由(I)得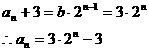 (Ⅲ)设存在s、p、r∈N*且s<p<r使as,ap,ar成等差数列∴2ap=as+ar∴
(Ⅲ)设存在s、p、r∈N*且s<p<r使as,ap,ar成等差数列∴2ap=as+ar∴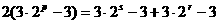
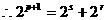 ………………9分
………………9分
即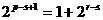 (*)∵s、p、r∈N*且s<p<r
(*)∵s、p、r∈N*且s<p<r
∴ 为奇数∴(*)为矛盾等式,不成立故这样的三项不存在。…12分
为奇数∴(*)为矛盾等式,不成立故这样的三项不存在。…12分
18.解证:(Ⅰ)连结AC、AF、BF、EF、
∵SA⊥平面ABCD
∴AF为Rt△SAC斜边SC上的中线
∴AF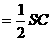 …………………………………2分
…………………………………2分
又∵ABCD是正方形∴CB⊥AB
而由SA⊥平面ABCD,得CB⊥SA
∴CB⊥平面SAB∴CB⊥SB
∴BF为Rt△SBC斜边SC上的中线
BF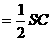 ……………………………………………………5分
……………………………………………………5分
∴△AFB为等腰三角形,EF⊥AB又CD//AB∴EF⊥CD……………………7分
(Ⅱ)由已知易得Rt△SAE≌Rt△CBE
∴SE=EC即△SEC是等腰三角形∴EF⊥SC
又∵SC∩CD=C∴EF⊥平面SCD又EF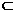 平面SCE
平面SCE
∴平面SCD⊥平面SCE……………………………………12分
17.解:(I)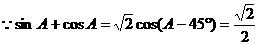
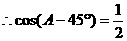 ……………………3分又∵0°<A<180°
……………………3分又∵0°<A<180°
∴A-45°=60°故A=105°………………………………5分
 ……………………7分
……………………7分
(Ⅱ)∵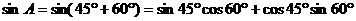
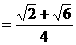 ………9分
………9分
∴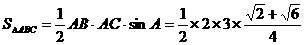
|
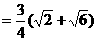 ……12分
……12分21.(本小题满分12分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(Ⅰ)试解释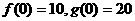 的实际意义;
的实际意义;
(Ⅱ)设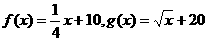 ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司应投入多少宣传费?
20.(本小题满分12分)
设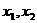 是函数
是函数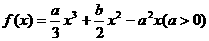 的两个极值点,且
的两个极值点,且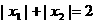
(Ⅰ)求a的取值范围;
(Ⅱ)求证: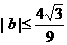 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com