
题目列表(包括答案和解析)
1、设集合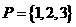 ,集合
,集合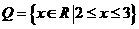 ,那么下列结论正确的是: ( )
,那么下列结论正确的是: ( )
A.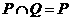 B.
B. 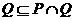 C.
C. 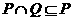 D.
D. 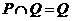
21.解:(1)由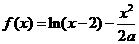 得
得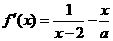 ……………………(1分)
……………………(1分)
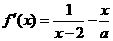
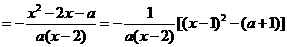
又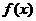 的定义域为
的定义域为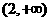 ,所以
,所以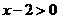
当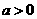 时,
时,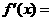

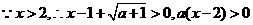
当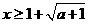 时,
时,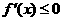 ,
,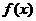 为减函数
为减函数
当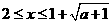 时,
时,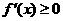 ,
,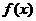 为增函数………………………(5分)
为增函数………………………(5分)
所以当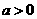 时,
时,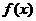 的单调递增区间为
的单调递增区间为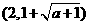
单调递减区间为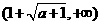 …………………(6分)
…………………(6分)
(2)由(1)知当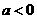 时,
时,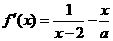
 ,
,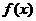 递增无极值………(7分)
递增无极值………(7分)
所以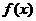 在
在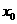 处有极值,故
处有极值,故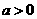 且
且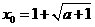
因为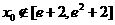 且
且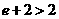 ,所以
,所以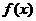 在
在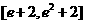 上单调
上单调
当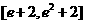 为增区间时,
为增区间时,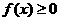 恒成立,则有
恒成立,则有
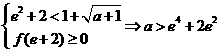 ………………………………………(9分)
………………………………………(9分)
当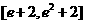 为减区间时,
为减区间时,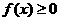 恒成立,则有
恒成立,则有
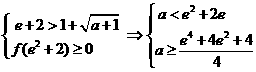 无解 ……………………(13分)
无解 ……………………(13分)
由上讨论得实数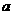 的取值范围为
的取值范围为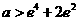 …………………………(14分)
…………………………(14分)
20.解:(1)将点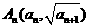 代入
代入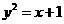 得
得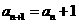
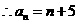
因为直线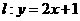 ,所以
,所以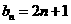 ……………………………………(3分)
……………………………………(3分)
(2)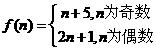 ,
,
当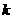 为偶数时,
为偶数时,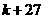 为奇数,
为奇数,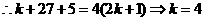 ……………(5分)
……………(5分)
当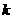 为奇数时,
为奇数时,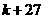 为偶数,
为偶数, (舍去)
(舍去)
综上,存在唯一的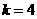 符合条件…………………………………………………(7分)
符合条件…………………………………………………(7分)
(3)证明不等式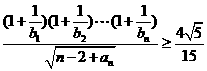 即证明
即证明
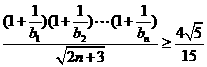 成立,下面用数学归纳法证明
成立,下面用数学归纳法证明
1当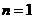 时,不等式左边=
时,不等式左边=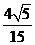 ,原不等式显然成立………………………(8分)
,原不等式显然成立………………………(8分)
2假设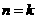
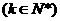 时,原不等式成立,即
时,原不等式成立,即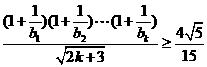
当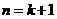 时
时
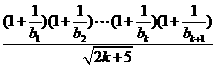 =
=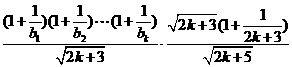
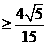
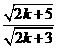
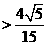 ,即
,即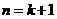 时,原不等式也成立 ………………(11分)
时,原不等式也成立 ………………(11分)
根据12所得,原不等式对一切自然数都成立 ……………………………(13分)
19.解:(1)当 时,
时,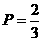 ,
,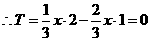 ……………………(2分)
……………………(2分)
当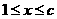 时,
时,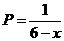 ,
,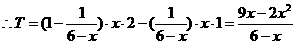
综上,日盈利额 (万元)与日产量
(万元)与日产量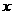 (万件)的函数关系为:
(万件)的函数关系为:
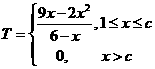 …………………………………………………………(4分)
…………………………………………………………(4分)
(2)由(1)知,当 时,每天的盈利额为0……………………………(6分)
时,每天的盈利额为0……………………………(6分)
当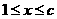 时,
时,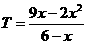
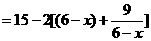
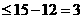
当且仅当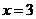 时取等号
时取等号
所以 当
当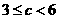 时,
时,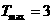 ,此时
,此时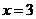 ……………………………(8分)
……………………………(8分)
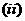 当
当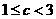 时,由
时,由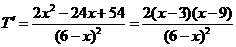 知
知
函数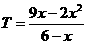 在
在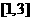 上递增,
上递增,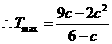 ,此时
,此时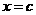 ……(10分)
……(10分)
综上,若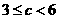 ,则当日产量为3万件时,可获得最大利润
,则当日产量为3万件时,可获得最大利润
若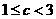 ,则当日产量为
,则当日产量为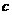 万件时,可获得最大利润…………(12分)
万件时,可获得最大利润…………(12分)
18.解:(1)当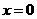 时,
时, ………………………(1分)
………………………(1分)
当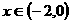 时,
时,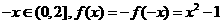 ……………………(2分)
……………………(2分)
由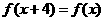 ,知
,知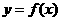 又是周期为4的函数,所以
又是周期为4的函数,所以
当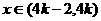 时
时
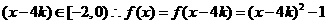 …………………………(4分)
…………………………(4分)
当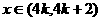 时
时
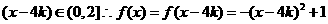 …………………………(6分)
…………………………(6分)
故当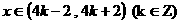 时,函数
时,函数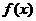 的解析式为
的解析式为
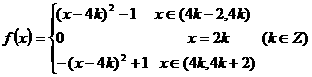 ………………………………(7分)
………………………………(7分)
(2)当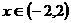 时,由
时,由 ,得
,得
 或
或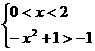 或
或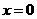
解上述两个不等式组得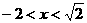 …………………………………………(10分)
…………………………………………(10分)
故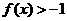 的解集为
的解集为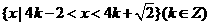 …………………(12分)
…………………(12分)
17.解:(1)由1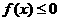 的解集有且只有一个元素知
的解集有且只有一个元素知
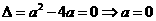 或
或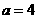 ………………………………………(2分)
………………………………………(2分)
当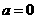 时,函数
时,函数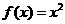 在
在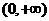 上递增,此时不满足条件2
上递增,此时不满足条件2
综上可知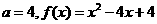 …………………………………………(3分)
…………………………………………(3分)
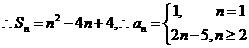 ……………………………………(6分)
……………………………………(6分)
(2)由条件可知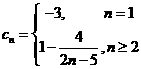 ……………………………………(7分)
……………………………………(7分)
当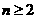 时,令
时,令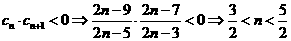 或
或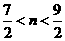
所以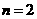 或
或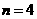 ……………………………………………………………(9分)
……………………………………………………………(9分)
又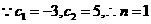 时,也有
时,也有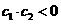 ……………………………(11分)
……………………………(11分)
综上可得数列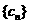 的变号数为3……………………………………………(12分)
的变号数为3……………………………………………(12分)
16.解:因为 ,所以
,所以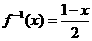 ………………………………(1分)
………………………………(1分)
由 得
得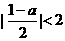 ,解得
,解得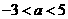 ………………………………(3分)
………………………………(3分)
因为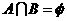 ,故集合
,故集合 应分为
应分为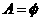 和
和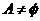 两种情况
两种情况
(1)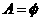 时,
时,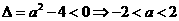 …………………………………(6分)
…………………………………(6分)
(2)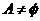 时,
时,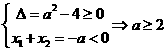 ……………………………………(8分)
……………………………………(8分)
所以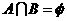 得
得 …………………………………………………(9分)
…………………………………………………(9分)
若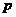 真
真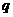 假,则
假,则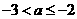 …………………………………………………………(10分)
…………………………………………………………(10分)
若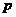 假
假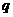 真,则
真,则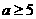 ……………………………………………………………(11分)
……………………………………………………………(11分)
故实数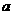 的取值范围为
的取值范围为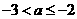 或
或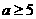 ………………………………………(12分)
………………………………………(12分)
11.2
12.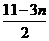 13.
13.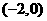 14.8 15.45
14.8 15.45
1~10 BADDA BCBCD
21.(本题满分14分)已知函数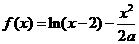 (
(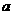 为常数且
为常数且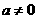 )
)
(1)当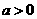 时,求
时,求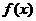 的单调区间
的单调区间
(2)若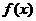 在
在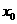 处取得极值,且
处取得极值,且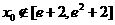 ,而
,而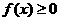 在
在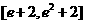 上恒成立,求实数
上恒成立,求实数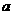 的取值范围(其中
的取值范围(其中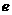 为自然对数的底数)
为自然对数的底数)
 2008届高三年级十月联考数学试题参考答案
2008届高三年级十月联考数学试题参考答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com