
题目列表(包括答案和解析)
7.函数f(x)=-x2+8x-16在区间[3,5]上 ( )
A.没有零点 B.有一个零点 C.有两个零点 D.无数个零点
6.可作为函数y=f(x)的图象的是 ( )
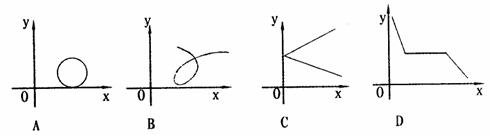
5.函数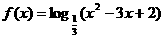 的单调递增区间为 ( )
的单调递增区间为 ( )
A.(-∞,1) B.(2,+∞) C.(-∞,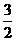 ) D.(
) D.(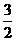 ,+∞)
,+∞)
4.函数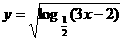 的定义域是 ( )
的定义域是 ( )
A.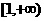 B.
B.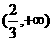 C.
C.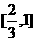 D.
D.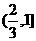
3.设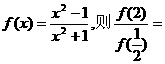 ( )
( )
A.1 B.-1 C.-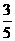 D.
D.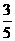
2.三个数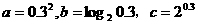 之间的大小关系是 ( )
之间的大小关系是 ( )
A.a<c<b B.a<b<c C.b<a<c D.b<c<a
1.设集合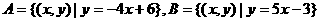 ,则
,则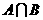 = ( )
= ( )
A.{1,2} B.{(1,2)} C.{x=1,y=2} D.(1,2)
(17)解:(Ⅰ)原式=lg22+(1- lg2)(1+lg2)-1
=lg22+1- lg22- 1=0
(Ⅱ)原式=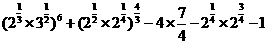
=22×33+2 - 7- 2- 1 =100
(18)解:(Ⅰ)设x<0,则- x>0, 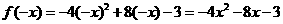 ∵f(x)是偶函数,
∵f(x)是偶函数,
∴f(-x)=f(x) ∴x<0时, 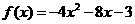
所以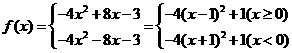
(Ⅱ)y=f(x)开口向下,所以y=f(x)有最大值f(1)=f(-1)=1
函数y=f(x)的单调递增区间是(-∞,-1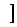 和[0,1]
和[0,1]
单调递减区间是 [-1,0]和[1,+∞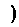
(19)解:设f(x)= ax2+bx+c (a≠0)
因为f(x)图象过点(0,3),所以c =3
又f(x)对称轴为x=2, ∴ 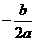 =2即b= - 4a
=2即b= - 4a
所以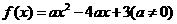
设方程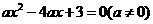 的两个实根为 x1,x2,
的两个实根为 x1,x2,
则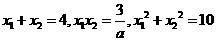
∴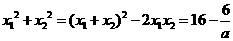 ,所以
,所以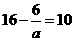
得a=1,b= - 4
所以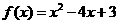
(20)证明:(Ⅰ)
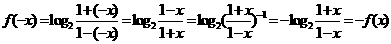
又x∈(-1,1),所以函数f(x)是奇函数
(Ⅱ)设 -1<x<1,△x=x2- x1>0
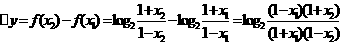
因为1- x1>1- x2>0;1+x2>1+x1>0
所以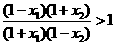
所以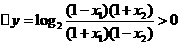
所以函数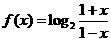 在(- 1,1)上是增函数
在(- 1,1)上是增函数
(21)(Ⅰ)设购买人数为n人,羊毛衫的标价为每件x元,利润为y元,
则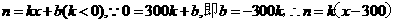
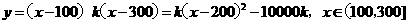
∵k<0,∴x=200时,ymax= - 10000k,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(Ⅱ)由题意得,k(x- 100)(x- 300)= - 10000k·75%

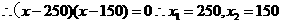
所以,商场要获取最大利润的75%,每件标价为250元或150元.
(13) (0,1)
(14){0,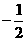 ,
,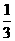 }
}
(15) 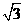 (16)
②③④
(16)
②③④
(17)计算下列各式
(Ⅰ)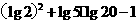 (Ⅱ)
(Ⅱ) 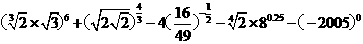
(18)定义在实数R上的函数y= f(x)是偶函数,当x≥0时,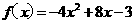 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
(19)已知二次函数f(x)图象过点(0,3),它的图象的对称轴为x = 2,
且f(x)的两个零点的平方和为10,求f(x)的解析式.
(20) 已知函数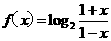 ,(x∈(- 1,1).
,(x∈(- 1,1).
(Ⅰ)判断f(x)的奇偶性,并证明;
(Ⅱ)判断f(x)在(- 1,1)上的单调性,并证明.
(21) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
2009届六安二中高三必修1复习卷( C)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com