
题目列表(包括答案和解析)
21、(1)证明:令-1≤x1<x2≤1,且a= x1,b=-x2
则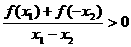 ∵x1- x2<0,f(x)是奇函数 ∴f(x1)-f(x2)<0即f(x1)<f(x2)
∵x1- x2<0,f(x)是奇函数 ∴f(x1)-f(x2)<0即f(x1)<f(x2)
∵x1<x2 ∴f(x)是增函数
(2)解:∵f(x)是增函数,且f(x)≤m2-2bm+1对所有x∈[-1,2]恒成立
∴[f(x)]max≤m2-2bm+1 [f(x)]max=f(1)=1
∴m2-2bm+1≥1即m2-2bm≥0在b∈[-1,1]恒成立
∴y= -2mb+m2在b∈[-1,1]恒大于等于0
∴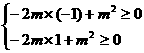 ,∴
,∴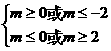
∴m的取值范围是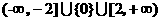
20、解:设摊主每天从报社买进x份,
显然当x∈[250,400]时,每月所获利润才能最大. 于是每月所获利润y为
y =20·0.30x+10·0.30·250+10·0.05·(x-250)-30·0.20x
=0.5x+625,x∈[250,400].
因函数y在[250,400]上为增函数,故当x = 400时,y有最大值825元.
19、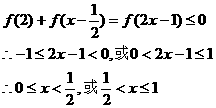 解:(1)①若a=0,则
解:(1)①若a=0,则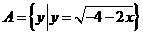 =
=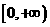 ,
,
②若a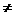 0,则
0,则 ;解得a>0
;解得a>0
综合①②得:a≥0。所以存在实数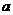 使
使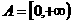 且
且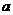 的取值范围是
的取值范围是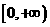
(2)B={x|ax2+2(a-1)x-4≥0}
①若a=0则B={x|-2x-4≥0}={x|x≤-2}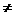
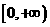
②若a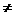 0则显然
0则显然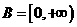 不可能成立
不可能成立
所以不存在实数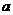 使
使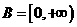
18、解:(1)令x=y=1,则f(1)=f(1)+ f(1) ∴f(1)=0
令x=y=-1,则f(1)=f(-1)+ f(-1) ∴f(-1)=0
 (2)令y=-1,则f(-x)=f(x)+f(-1)=f(x) ∴f(-x)=f(x)
(2)令y=-1,则f(-x)=f(x)+f(-1)=f(x) ∴f(-x)=f(x)
(3)据题意可知,函数图象大致如下:
17、解:(1)令t=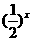 ,则y=t2-t+1=(t-
,则y=t2-t+1=(t-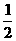 )2+
)2+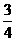
当时x∈[1,2],t=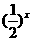 是减函数,此时t
是减函数,此时t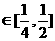 ,y=t2-t+1是减函数
,y=t2-t+1是减函数
当时x∈[-3,1],t=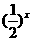 是减函数,此时t
是减函数,此时t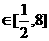 ,y=t2-t+1是增函数
,y=t2-t+1是增函数
∴函数的单调增区间为[1,2],单调减区间为[-3,1]
(2)∵x∈[-3,2],∴t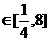 ∴值域为
∴值域为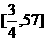
11、{0,3} 12、(-1,-1) 13、2400 14、2 15、-1或2 16、①⑤
21、已知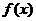 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当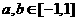 ,且
,且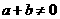 时有
时有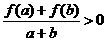 .
.
(1)判断函数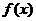 的单调性,并给予证明;
的单调性,并给予证明;
(2)若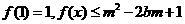 对所有
对所有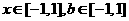 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
2009届六安二中高三文1、2、8班必修1复习卷(E) 答案
20、某市的一家报刊摊点,从报社买进《晚报》的价格是每份0.20元,卖出价是每份0.30元,卖不掉的报纸可以以每份0.05元价格退回报社.在一个月(以30天计)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
19.(1)已知集合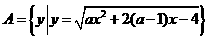 ,是否存在实数
,是否存在实数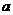 使
使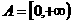 ?若存在,求出
?若存在,求出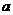 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(2)若集合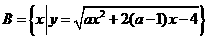 ,是否存在实数
,是否存在实数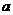 使
使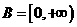 ?若存在,求出
?若存在,求出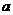 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
18.定义在非零实数集上的函数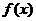 满足
满足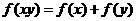 ,且
,且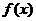 是区间
是区间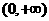 上的递增函数. (1)求:
上的递增函数. (1)求: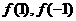 的值;(2)求证:
的值;(2)求证: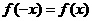 ;(3)解不等式
;(3)解不等式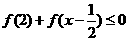 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com