
题目列表(包括答案和解析)
(13)函数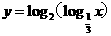 的定义域为
.
的定义域为
.
(14)若集合M={x| x2+x-6=0},N={x| kx+1=0},且N M,则k的可能值组成的集合为
.
M,则k的可能值组成的集合为
.
(15)设函数 ,若f(x)=3,则x= .
,若f(x)=3,则x= .
(16)有以下4个命题:
①函数f(x)= ax(a>0且a≠1)与函数g(x)=log aax(a>0且a≠1)的定义域相同;
②函数f(x)=x3与函数g(x)=3 x的值域相同;
③函数f(x)=(x-1)2与g(x)=2 x -1在(0,+∞)上都是增函数;
④如果函数f(x)有反函数f -1(x),则f(x+1)的反函数是f -1(x+1).
其中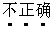 的题号为
.
的题号为
.
(1)若集合A={1,3,x},B={1,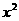 },A∪B={1,3,x},则满足条件的实数x的个数有( )
},A∪B={1,3,x},则满足条件的实数x的个数有( )
(A) 1个 (B) 2个 (C)3个 (D) 4个
(2)集合M={(x,y)| x>0,y>0},N={(x,y)| x+y>0,xy>0}则( )
(A)M=N (B)M 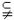 N (C)M
N (C)M 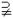 N (D)M
N (D)M N=
N=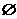
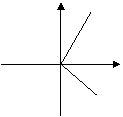
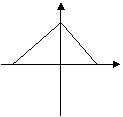 (3)下列图象中不能表示函数的图象的是 ( )
(3)下列图象中不能表示函数的图象的是 ( )
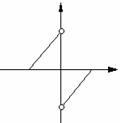
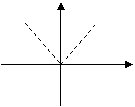 y
y
y
y
y
y
o x x o x o x
(A) (B) (C) (D)
(4)若函数y=f(x)的定义域是[2,4],则y=f(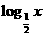 )的定义域是( )
)的定义域是( )
(A) [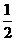 ,1] (B) [4,16] (C)[
,1] (B) [4,16] (C)[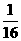 ,
,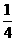 ] (D)[2,4 ]
] (D)[2,4 ]
(5)函数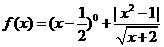 的定义域为( )
的定义域为( )
(A)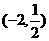 (B)(-2,+∞)
(C)
(B)(-2,+∞)
(C)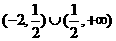 (D)
(D)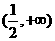
(6)设偶函数f(x)的定义域为R,当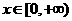 时f(x)是增函数,则
时f(x)是增函数,则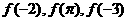 的大小关系是( )
的大小关系是( )
(A)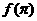 >
> >
>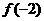 (B)
(B)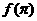 >
>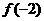 >
>
(C)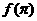 <
< <
<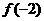 (D)
(D)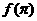 <
<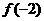 <
<
(7)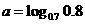 ,
,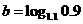 ,
,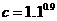 ,那么( )
,那么( )
(A)a<b<c (B)a<c<b (C)b<a<c (D)c<a<b
 (8)已知函数
(8)已知函数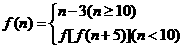 ,其中n
,其中n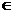 N,则f(8)=( ) C
N,则f(8)=( ) C
(A)6 (B)7 (C) 2 (D)4
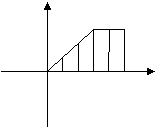
(9)某工厂今年前五个月每月生产某种产品的数量C(件)关于时间
t(月)的函数图象如图所示,则这个工厂对这种产品来说( ) O 一二 三 四五 t
(A)一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少
(B)一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平
(C)一至三月每月生产数量逐月增加,四、五两月均停止生产
(D)一至三月每月生产数量不变,四、五两月均停止生产
(10)若函数f(x)和g(x)都为奇函数,函数F(x)=af(x)+bg(x)+3在(0,+∞)上有最大值10,则F(x)在(-∞,0)上有( )
(A) 最小值 -10 (B)最小值 -7 (C)最小值 -4 (D)最大值 -10
(11)若函数 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( )
(A)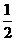 (B)
(B)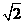 (C)
(C)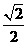 (D)2
(D)2
(12)如果二次函数f(x)=3x2+bx+1在(-∞,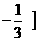 上是减函数,在
上是减函数,在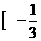 ,+∞)上是增函数,则f(x)的最小值为( )
,+∞)上是增函数,则f(x)的最小值为( )
(A)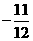 (B)
(B)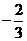 (C)
(C)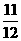 (D)
(D)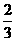
22、某电器公司生产A型电脑。1993年这种电脑每台平均生产成本为5 000元,并以纯利润20%确定出厂价。从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低。到1997年,尽管A型电脑出厂价仅是1993年的80%,但却实现了50%纯利润的高效益。
(1)求1997年每台A型电脑的生产成本;
(2)以1993年的生产成本为基数,求1993-1997年生产成本平均每年降低的百分数(精确到0.01,以下数据可供参考: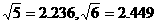 )。
)。
21、如图,已知底角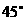 的等腰梯形ABCD,底边BC长为7cm,腰长为
的等腰梯形ABCD,底边BC长为7cm,腰长为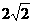 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=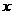 ,试写出左边部分的面积
,试写出左边部分的面积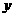 与
与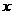 的函数解析式,并画出大致图象。
的函数解析式,并画出大致图象。
 L A
D
L A
D



E
B F G H B
20、已知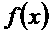 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当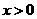 时,f(x)=log2x求
时,f(x)=log2x求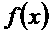 的解析式。
的解析式。
19、已知函数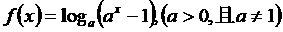 ,
,
(1)求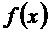 的定义域; (2)讨论函数
的定义域; (2)讨论函数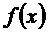 的单调性。
的单调性。
18、设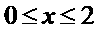 ,求函数
,求函数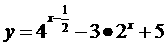 的最大值与最小值。
的最大值与最小值。
17、求函数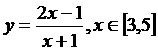 的最小值和最大值。
的最小值和最大值。
16、1992年底世界人口达到54.8亿,若人口的平均增长率为1%,经过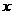 年后世界人口数为
年后世界人口数为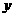 (亿),则
(亿),则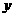 与
与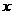 的函数解析式为
的函数解析式为
15、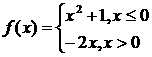 若
若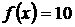 ,则
,则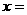
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com