
题目列表(包括答案和解析)
8.已知函数 ,
, 。规定:给定一个实数
。规定:给定一个实数 ,赋值
,赋值 ,若
,若 ,则继续赋值
,则继续赋值 ,…,以此类推,若
,…,以此类推,若 ,则
,则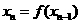 ,否则停止赋值,如果得到
,否则停止赋值,如果得到 称为赋值了
称为赋值了 次(
次( )。已知赋值
)。已知赋值 次后该过程停止,则
次后该过程停止,则 的取值范围是( )
的取值范围是( )
A. B.
B.
C.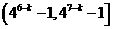 D.
D.
7.设 ,
, ,
,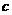 均为正数,且
均为正数,且 ,
, ,
, ,则( )
,则( )
A. B.
B. C.
C. D.
D.
6.设随机变量 -
- ,且当二次方程
,且当二次方程 无实根时的
无实根时的 的取值概率为0.5,则
的取值概率为0.5,则 ( )
( )
A.0 B.0.5 C.1 D.2
5.四面体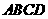 的外接球球心在
的外接球球心在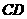 上,且
上,且 ,
, ,则在外接球球面上
,则在外接球球面上 ,
, 两点间的球面距离是( )
两点间的球面距离是( )
A.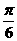 B.
B. C.
C. D.
D.
4.在平面直角坐标系 中,已知
中,已知 顶点
顶点 和
和 ,顶点
,顶点 在椭圆
在椭圆 上,则
上,则 的值是( )
的值是( )
A. B.
B. C.
C. D.与点
D.与点 位置有关
位置有关
3.已知对任意实数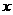 ,有
,有 ,
, ,且
,且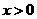 时,
时, ,
, ,则
,则 时,有( )
时,有( )
A. ,
, B.
B. ,
,
C. ,
, D.
D. ,
,
2.在等差数列 中,若
中,若 ,则
,则 ( )
( )
A. B.
B.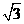 C.
C. D.
D.
1.定义集合M与N的新运算: ,若
,若 ,
, ,则
,则 等于( )
等于( )
A.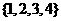 B.
B. C.
C. D.
D.
22. (本题 12分) 设数列 的前
的前 项和为
项和为 ,对一切
,对一切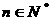 ,点
,点 都在函数
都在函数 的图像上。
的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)将数列 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为
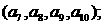
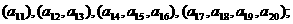
 分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列 ,求
,求
(Ⅲ)设 为数列
为数列 的前
的前 项积,是否存在实数
项积,是否存在实数 ,使得不等式
,使得不等式 对一切
对一切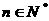 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
解:(Ⅰ)(法一)猜想,数学归纳法证明; ----------------------------4分
----------------------------4分
(II)因为 ,所以数列
,所以数列 依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….每一次循环记为一组.由于每一个循环含有4个括号,故
依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….每一次循环记为一组.由于每一个循环含有4个括号,故 是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,所以
是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,所以 =68+24+80=1988.又
=68+24+80=1988.又 =22,所以
=22,所以 =2010.-------------8分
=2010.-------------8分
(III)(理)因为 ,故
,故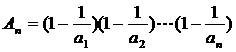 ,
,
所以 .
.
又 ,
,
故 对一切
对一切 都成立,就是
都成立,就是
 对一切
对一切 都成立.--------------10分
都成立.--------------10分
设 ,则只需
,则只需 即可.
即可.
由于 ,
,
所以 ,故
,故 是单调递减,于是
是单调递减,于是 .
.
令 ,即
,即 ,
,
解得 ,或
,或 .
.
综上所诉,使得所给不等式对一切 都成立的实数
都成立的实数 存在,
存在, 的取值范围是
的取值范围是 .-------------------------------------------------------12分
.-------------------------------------------------------12分
本资料由《七彩教育网》 提供!
21.解:(1)由椭圆方程 及双曲线方程
及双曲线方程 可得点
可得点 直线
直线 方程是
方程是
 且
且 在直线
在直线 上运动。
上运动。
可设
则 的垂直平分线方程为
的垂直平分线方程为 ①
①
 的垂直平分线方程为
的垂直平分线方程为 ②
②
 P是△ABC的外接圆圆心,
P是△ABC的外接圆圆心, 点P的坐标
点P的坐标 满足方程①和②
满足方程①和②
由①和②联立消去 得
得
故圆心P的轨迹E的方程为 ---------------------------------------------------------6分
---------------------------------------------------------6分
(2)由图可知,直线 和
和 的斜率存在且不为零,设
的斜率存在且不为零,设 的方程为
的方程为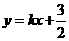 ,
,
 ,
,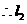 的方程为
的方程为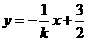
由
得  ------------------------------8分
------------------------------8分
 △=
△= 直线
直线 与轨迹E交于两点。
与轨迹E交于两点。
设 ,则
,则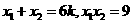 。
。

同理可得:
 四边形MRNQ的面积
四边形MRNQ的面积
 -----------------10分
-----------------10分
当且仅当 ,即
,即 时,等号成立。
时,等号成立。
故四边形MNRQ的面积的最小值为72。------------------------------------------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com