
题目列表(包括答案和解析)
1、复数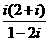 等于( D )
等于( D )
A.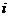 B.
B.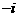 C.1 D.
C.1 D.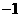
22、设椭圆C: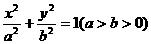 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且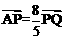 .
.
 ⑴求椭圆C的离心率;
⑴求椭圆C的离心率;
⑵若过A、Q、F三点的圆恰好与直线l:
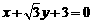 相切,求椭圆C的方程.
相切,求椭圆C的方程.
21、已知定义在R上的单调函数y=f(x),当x<0时,f(x)>1,且对任意的实数x、y∈R,有f(x+y)=f(x)f(y),
(Ⅰ)求f(0),并写出适合条件的函数f(x)的一个解析式;
(Ⅱ)数列{an}满足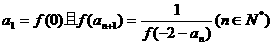 ,
,
①求通项公式an的表达式;
②令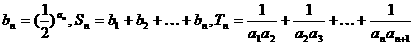 ,
,
试比较Sn与 Tn的大小,并加以证明.
Tn的大小,并加以证明.
20、有A,B,C,D四个城市,它们都有一个著名的旅游点,依此记为a,b,c,d.把ABCD和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右两边的字母全部连接起来,构成“一一对应”,已知每连对一个得2分,连错得0分;
(Ⅰ)求该爱好者得分的分布列;
(Ⅱ)求该爱好者得分的数期望.
19、已知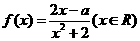 在区间
在区间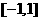 上是增函数
上是增函数
(I)求实数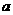 的取值范围;
的取值范围;
(II)记实数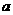 的取值范围为集合A,且设关于
的取值范围为集合A,且设关于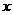 的方程
的方程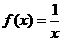 的两个非零实根为
的两个非零实根为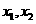 。
。
①求 的最大值;
的最大值;
②试问:是否存在实数m,使得不等式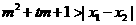 对
对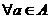 及
及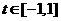 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
18、如图,在矩形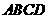 中,
中,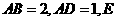 是
是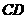 的中点,以
的中点,以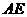 为折痕将
为折痕将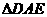 向上折起,使
向上折起,使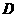 为
为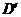 ,且平面
,且平面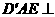 平面
平面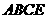 .
.
(Ⅰ)求证: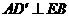 ;
;
(Ⅱ)求直线 与平面
与平面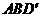 所成角的正弦值.
所成角的正弦值.
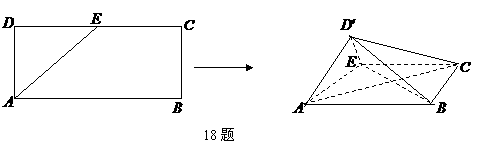

17、已知三点A,B,C的坐标分别为 ,且
,且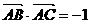
(1)求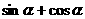 的值;(2)求
的值;(2)求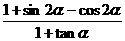 的值。
的值。
16、已知两个点M(-5,0)和N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”,给出下列直线:①y=x+1,②y= x, ③y=2,④y=2x+1,其中为“B型直线”的是 .(填上所有正确结论的序号)
x, ③y=2,④y=2x+1,其中为“B型直线”的是 .(填上所有正确结论的序号)
15、若函数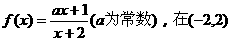 内为增函数,则实数a的取值范围 ;
内为增函数,则实数a的取值范围 ;
14、先后抛掷两枚均匀的正方体骰子,骰子朝上的面的点数为a、b,则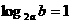 的概率为 .
的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com