
题目列表(包括答案和解析)
20.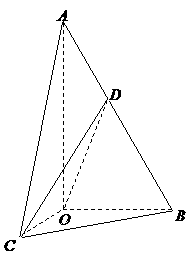 解法一:
解法一:
(I)由题意,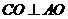 ,
,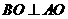 ,
,
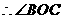 是二面角
是二面角 的平面角,
的平面角,
又 二面角
二面角 是直二面角,
是直二面角,
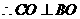 ,又
,又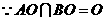 ,
,
 平面
平面 ,
,
又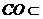 平面
平面 .
.
 平面
平面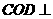 平面
平面 .--------------------------------------------------------4分
.--------------------------------------------------------4分
(II)作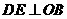 ,垂足为
,垂足为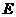 ,连结
,连结 (如图),则
(如图),则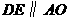 ,
,
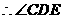 是异面直线
是异面直线 与
与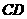 所成的角.----------------------------------5分
所成的角.----------------------------------5分
在 中,
中,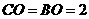 ,
,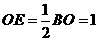 ,
,
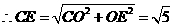 .
.
又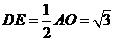 .
.
 在
在 中,
中,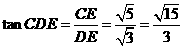 .---------------------------------------7分
.---------------------------------------7分
 异面直线
异面直线 与
与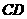 所成角的大小为
所成角的大小为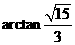 .---------------------------------------8分
.---------------------------------------8分
(III)由(I)知, 平面
平面 ,
,
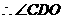 是
是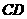 与平面
与平面 所成的角,且
所成的角,且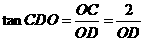 .
.
当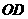 最小时,
最小时, 最大,------------------------------------10分
最大,------------------------------------10分
这时,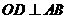 ,垂足为
,垂足为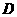 ,
,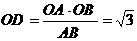 ,
,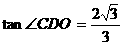 ,
,
 与平面
与平面 所成角的最大值为
所成角的最大值为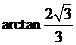 .-----------------------------12分
.-----------------------------12分
19.解:(1)依题意,得: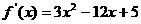 ,
, ,得
,得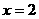
所以拐点坐标是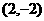 …………………
3分
…………………
3分
(2方法一:由(1)知“拐点”坐标是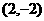 ,而
,而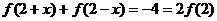 ,所以
,所以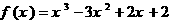 关于点
关于点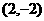 对称。
对称。
方法二:设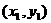 与
与 关于
关于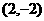 中心对称,并且
中心对称,并且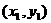 在
在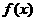 ,所以就有
,所以就有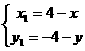 ,由
,由 ,得
,得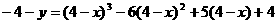
化简的: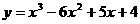
所以点 也在
也在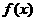 上,故
上,故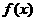 关于点
关于点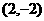 对称。
………………… 7分
对称。
………………… 7分
一般的,三次函数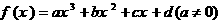 的“拐点”是
的“拐点”是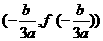 ,它就是函数
,它就是函数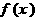 的对称中心(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数。。。。。。。)都可以给分。
…………………
10分
的对称中心(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数。。。。。。。)都可以给分。
…………………
10分
(3)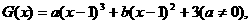 或写出一个具体函数,如
或写出一个具体函数,如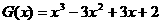 ,或
,或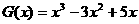 …………………
12分
…………………
12分
实质:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;且任何一个三次函数的“拐点”就是它的对称中心,即: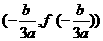
18.解:既会唱歌又会跳舞的有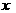 人,则文娱队中共有(7-
人,则文娱队中共有(7-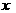 )人,
)人,
那么只会一项的人数是(7-2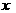 )人
)人
(1) 由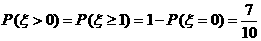
所以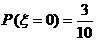 即
即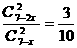 解得
解得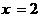
故文娱队共有5人.---------------------------------------------------------------------------------4分
(2) 可能取得值为:0,1,2-------------------------------------------------------------6分
可能取得值为:0,1,2-------------------------------------------------------------6分
则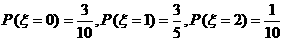 -----------------------------------------8分
-----------------------------------------8分
 的分布列为
的分布列为
 |
0 |
1 |
2 |
|
P |
3/10 |
3/5 |
1/10 |
---------------------------------------------------10分
则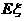 =
= -----------------------------------------------------------------------12分
-----------------------------------------------------------------------12分
17.解由条件得
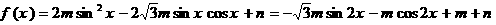
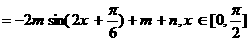 --------------------------------4分
--------------------------------4分
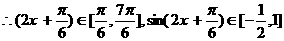 --------------------------6分
--------------------------6分
当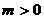 时,
时,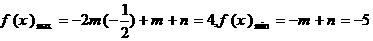
解得: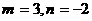 ,从而
,从而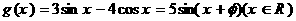
所以最大值为5,最小值为-5。---------------------------------------8分
当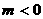 时,
解得
时,
解得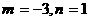 ,
,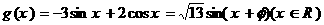
所以最大值为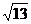 ,最小值为
,最小值为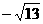 。--------------------------------10分
。--------------------------------10分
13. 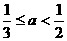 14.
14. 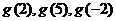 15. 1 16.
15. 1 16. 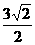
22. (本题 12分) 设数列 的前
的前 项和为
项和为 ,对一切
,对一切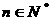 ,点
,点 都在函数
都在函数 的图像上。
的图像上。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)将数列 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为
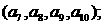
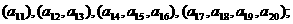
 分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列 ,求
,求
(Ⅲ)设 为数列
为数列 的前
的前 项积,是否存在实数
项积,是否存在实数 ,使得不等式
,使得不等式 对一切
对一切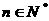 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
2008-2009学年度第二学期期中考试高三年级数学试卷 (理科)
一:选择题:BACCB AACAC DA
21.(本题满分 12分)△ABC中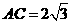 ,B是椭圆
,B是椭圆 在x轴上方的顶点,
在x轴上方的顶点, 是双曲线
是双曲线 位于x轴下方的准线,当AC在直线
位于x轴下方的准线,当AC在直线 上运动时。
上运动时。
(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点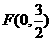 作互相垂直的直线
作互相垂直的直线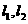 ,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
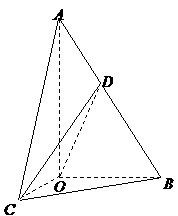
20. (本题满分12分) 如图,在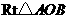 中,
中,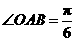 ,斜边
,斜边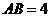 .
.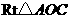 可以通过
可以通过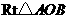 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点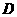 的斜边
的斜边 上.
上.
(I)求证:平面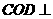 平面
平面 ;
;
(II)当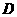 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与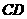 所成角的大小;
所成角的大小;
(III)求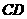 与平面
与平面 所成角的最大值.
所成角的最大值.
19.(本题满分12分)对于三次函数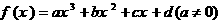
定义:设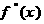 是函数
是函数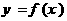 的导数
的导数 的导数,若方程
的导数,若方程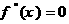 有实数解
有实数解 ,则称点
,则称点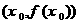 为函数
为函数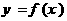 的“拐点”;
的“拐点”;
已知函数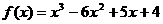 ,请回答下列问题;(1)求函数
,请回答下列问题;(1)求函数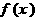 的“拐点”
的“拐点”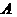 的坐标
的坐标
(2)
 检验函数
检验函数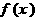 的图像是否关于“拐点”
的图像是否关于“拐点”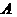 对称,对于任意的三次函数写出一个有关“拐点”的结论;(3)写出一个三次函数
对称,对于任意的三次函数写出一个有关“拐点”的结论;(3)写出一个三次函数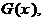 使得它的“拐点”是
使得它的“拐点”是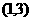 (不要过程)
(不要过程)
18. (本题满分12分) 学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人,设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且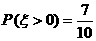
(1) 求文娱队的人数;
(2) 写出 的概率分布列并计算
的概率分布列并计算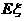 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com