
题目列表(包括答案和解析)
10、各项均为正数的等比数列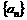 的前n项和为Sn,若Sn=2,S30=14,则S40等于( )
的前n项和为Sn,若Sn=2,S30=14,则S40等于( )
(A)80 (B)30 (C)26 (D)16
9、要得到函数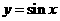 的图象,只需将函数
的图象,只需将函数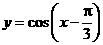 的图象( )
的图象( )
A.向右平移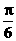 个单位 B.向右平移
个单位 B.向右平移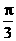 个单位
个单位
C.向左平移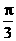 个单位 D.向左平移
个单位 D.向左平移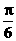 个单位
个单位
8、已知向量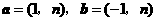 ,若
,若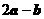 与
与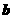 垂直,则
垂直,则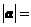 ( )
( )
A.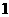 B.
B.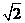 C.
C.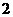 D.4
D.4
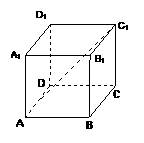
7、在正方体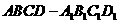 中,
中,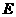 是
是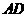 的中点,
的中点,
则异面直线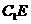 与
与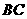 所成的角的余弦值是( )
所成的角的余弦值是( )
 A.
A. B.
B.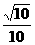
C.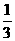 D.
D.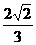
5、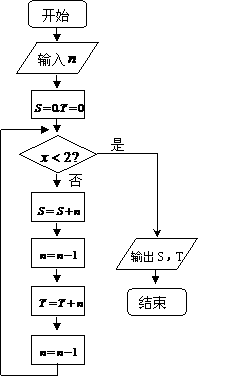 设
设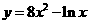 , 则此函数在区间
, 则此函数在区间  和
和 内分别为 ( )
内分别为 ( )
A.单调递增,单调递增 B.单调递增,单调递减
C.单调递减,单调递增 D.单调递减,单调递减
4、极坐标系中,圆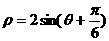 的圆心坐标是 ( )
的圆心坐标是 ( )
A.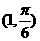 B.
B.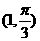 C.
C.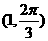 D.
D.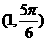
3、下列几何体各自的三视图中,有且仅有两个视图相同的是( )

A.①② B.①③ C.①④ D.②④
A.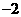 B.
B.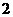 C.3 D.
C.3 D.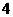
2、已知集合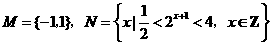 ,则
,则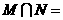 ( )
( )
A.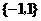 B.
B. C.
C.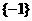 D.
D.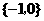
10. 已知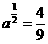 (a>0) ,则
(a>0) ,则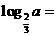 .
.
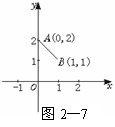 11,
11,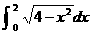 =_____________。
=_____________。
12,设函数y=f(x)满足:对任意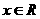 ,
,
① 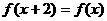 ,②
,② 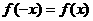 ,
,
③ 它在区间[0,1]上的图象为如图2-7所示
的线段AB,则在区间[3,4]上f(x)= . (写出表达式)
13,函数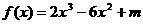 (
( 为常数)在
为常数)在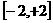 上有最大值
上有最大值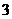 ,那么此函数在
,那么此函数在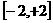 上的最小值为
上的最小值为
14, 给出下列四个命题:
①函数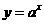 (
(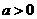 且
且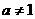 )与函数
)与函数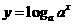 (
(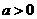 且
且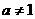 )的定义域相同;
)的定义域相同;
②函数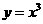 与
与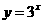 的值域相同;
的值域相同;
③函数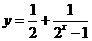 与
与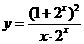 都是奇函数;
都是奇函数;
④函数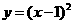 与
与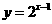 在区间
在区间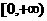 上都是增函数,
上都是增函数,
其中正确命题的序号是 .(把你认为正确的命题序号都填上)
三 解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程和演算步骤
15, (本题满分12分)
函数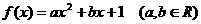 ,
,
(Ⅰ)若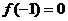 ,且对任意实数
,且对任意实数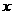 均有
均有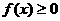 成立,求
成立,求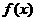 的表达式. (6分)
的表达式. (6分)
(Ⅱ)在(Ⅰ)的条件下,当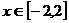 时,
时,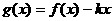 是单调递增函数,求实数
是单调递增函数,求实数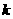 的取值范围。 (6分)
的取值范围。 (6分)
16,(本小题满分12分)
已知函数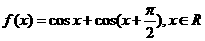
(Ⅰ)求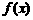 的最小正周期; (3分)
的最小正周期; (3分)
(Ⅱ)求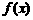 的单调增区间; (4分)
的单调增区间; (4分)
(Ⅲ)若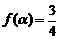 ,求
,求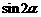 的值. (5分)
的值. (5分)
17,(本小题满分14分)
甲、乙两人各射击一次,击中目标的概率分别是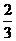 和
和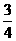 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(Ⅰ) 求甲射击4次,至少1次未击中目标的概率;
(3分)
(Ⅱ) 求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(5分)
(Ⅲ) 假设某人连续2次未击中目标,则停止射击. 问: 乙恰好射击5次后,被中止射击的概率是多少? (6分)
18,(本小题满分14分)
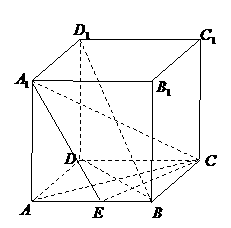 如图,正方体
如图,正方体 的棱长为2,
的棱长为2,
E为AB的中点.
(Ⅰ) 求异面直线BD1与CE所成角的余弦值;
(3分)
(Ⅱ) 求二面角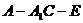 的余弦值;
的余弦值;
(5分)
(Ⅲ)求点B到平面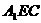 的距离;
的距离;
(6分)
19,(本小题满分14分)
设函数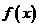 的定义域是
的定义域是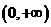 ,对任意正实数
,对任意正实数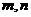 恒有
恒有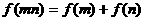 ,且当
,且当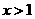 时,
时,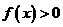 ,
,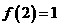
(Ⅰ) 求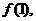
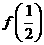 ,
,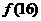 的值; (3分)
的值; (3分)
(Ⅱ) 求证: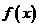 在
在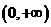 上是增函数; (5分)
上是增函数; (5分)
(Ⅲ) 求方程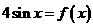 的根的个数.
(6分)
的根的个数.
(6分)
20,(本小题满分14分)
已知函数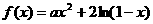 (
(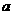 为实数).
为实数).
(I)若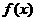 在
在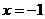 处有极值,求
处有极值,求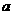 的值;
(3分)
的值;
(3分)
(II)若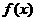 在
在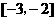 上是增函数,求
上是增函数,求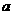 的取值范围. (11分)
的取值范围. (11分)


数学(理)试卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com