
题目列表(包括答案和解析)
20.(本小题12分)
(理科答)A、B两队进行篮球决赛,共五局比赛,先胜三局者夺冠,且比赛结束。根据以往成绩,每场中A队胜的概率为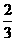 ,设各场比赛的胜负相互独立.
,设各场比赛的胜负相互独立.
(1)求A队夺冠的概率;
(2)设随机变量ξ表示比赛结束时的场数,求Eξ.
(文科答)甲、乙在罚球线投球命中的概率分别为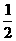 与
与
(1)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球两次,求这四次投球中至少一次命中的概率.
19.(本小题12分)
如图,正三棱柱ABC-A1B1C1中,D、E分别是BC、CC1的中点,AB=AA1.
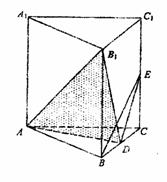 (1)求二面角B-AD-B1的正切值;
(1)求二面角B-AD-B1的正切值;
(2)证明:BE⊥平面AB1D;
(3)求异面直线DE与A1B1所成角的大小.
18.(本小题12分)
已知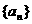 是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
是等比数列,Sn是其前n项的和,a1,a7,a4成等差数列,求证:2S3,S6,S12-S6,成等比数列.
17.(本题12分)
已知点A(2,0)、B(0,2)、C(cosα,sinα),O为坐标原点,且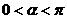 .
.
(1)若 ,求
,求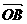 与
与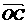 的夹角;
的夹角;
(2)若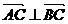 ,求tanα的值.
,求tanα的值.
|
16.已知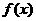 是定义在R上的奇函数,且是周期为2的周期函数,当
是定义在R上的奇函数,且是周期为2的周期函数,当 时,
时,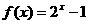 ,则
,则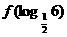 的值为
.
的值为
.
15.从0,1,2,3,4,5,6,7,8,9中取出3个数,使其和为不小于10的偶数,不同的取法共有 种(用数字作答).
14.若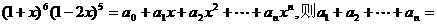 .
.
13.设函数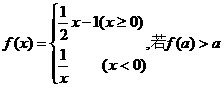 ,则实数
,则实数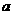 的取值范围是
.
的取值范围是
.
12.已知P是以F1、F2为焦点的双曲线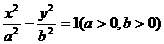 上的一点,若
上的一点,若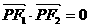 ,tan
,tan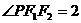 ,则此双曲线的离心率为 ( )
,则此双曲线的离心率为 ( )
A.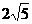 B.3 C.5 D.
B.3 C.5 D.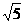
第II卷(非选择题,共90分)
11.(理科答)甲、乙两名篮球队员轮流投篮至某人投中为止。设每次投篮甲投中的概率为0.4,乙投中的概率为0.6,而且不受其他投篮结果的影响。设甲投篮次数为ξ,且甲先投,则P(ξ=k)= ( )
A.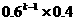 B.
B.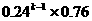 C.
C.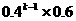 D.
D.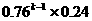
(文科答)要从10名女生与5名男生中选出6名学生组成课外学习小组,如果按性别分层随机抽样,则组成此课外学习小组的概率为 ( )
A.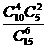 B.
B.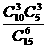 C.
C.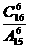 D.
D.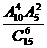
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com